I am a student at Wolfram Summer School 2016. This is the project I did about the evolution of the code 1599 cellular automaton.
Introduction to the code 1599 cellular automaton
Code 1599 is a 3-color totalistic cellular automaton. With radius 1, its rule looks like this:

The rule looks very simple. However, when the simple rule combines with simple initial conditions, very complex and interesting behaviors can arise.



This is the patterns produced by code 1599 starting from a single black cell in a uniform white background. What makes this complicated evolving pattern more interesting is that it will eventually turn to repetitive patterns after nearly 10000 steps. We do not know if all initial conditions will eventually die out, or if they do, at what steps. This is the open problem.
In his book A New Kind of Science, Stephen Wolfram described code 1599 as having a "free will" pattern, and used it as an example of his idea of computational irreducibility.
Approaching the problem
In this project, we try to find a way to predict the long-term evolution code 1599 cellular automaton given only very small steps. We accomplished this by separating the status of the cellular automaton into three classes: dead, oscillates and evolving, and using a classifier to make predictions. The features of different status are extracted and represented as tensors. Using the default training set we currently have, the classifier function is able to accurately predict the status after 50000 steps by only looking at the first 1000 steps. Below is some sample test results of the prediction function:
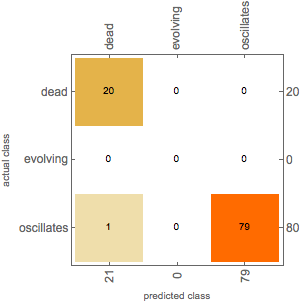
- Test 1: 100 Random initial conditions of size 6, Labeled after 30000 steps. (the test set is labeled after run for 30000, the prediction function only use the first 1000 steps to predict).
- Test2: 100 Random initial conditions of size 31, Labeled after 50000 steps.
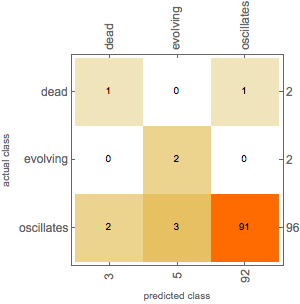
As we can see, not only does the classifier function have a high overall accuracy, but it also makes the right prediction on the rare cases of dead and evolving. So with the default training set. we have a classifier function that can accurately predict the status of the code 1599 after 50000 steps. We might be able to make predictions for larger steps if we use better training set.
Prediction Result
We used the prediction function on 534 initial conditions of random sizes ranging from 6 to 41, and get a prediction of 476 oscillates, 53 dead, and 5 cases of evolving. When we examine the 5 evolving initial conditions and run them to longer steps, about 100000, all of them turn to repetitive patterns. This seems to suggest that all evolving patterns will eventually turn to repetitive patterns. However, we cannot make conclusions since our classifier function is only as good as the labeled training set, and more test data is needed.
Conclusion
We have built a prediction function that can accurately predict the long-term behavior of the code 1599 cellular automaton, given only its initial condition run to 1000 steps. Using the default training set we can accurately predict status after 50000 steps. We can predict for larger steps if we provide training set labeled after larger steps. However, the limitation of the prediction function is that it is only as good as the labeled training set, so we cannot make definite conlusions about if all code 1599 evolving patterns will eventually turn to repetitive.
Future Direction - A suprising discovery
When finishing the prediction function, I played around with the rule by expanded the search space to initial conditions with repetitive backgrounds instead of just uniform ones, and I found some very interesting and surprising new patterns that resemble some of the elementary cellular automaton rules.
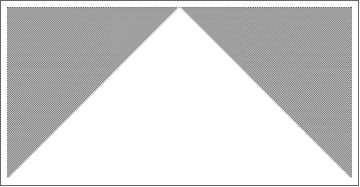
- Rule 150 Elementary Cellular automaton-like nested structure

- Rule 30 Elementary Cellular automaton-like chaotic pattern (the left edge of the triangle)

The next direction of our project would be to understand why using more complex initial conditions we would produce simple patterns resemble elementary rules that are not at all equivalent to code 1599.