Abstract

Recent development in machine intelligence has proved neural network' s capacity of handling a spectrum of tasks. Neural Networks of different structure has different fortes. For example, convolutional neural network is efficient in visual pattern recognition. In this project, I try more than a thousand architectures of neural network to learn arithmetic operations(addition and multiplication). Does the network of greatest depth and width perform the best? So far there' s some interesting conclusions.

A Brief Review of Neural Networks

Each neuron performs a linear transformation or a non - linear activation function to its input, so that information is updated through layers. In each dotpluslayer, the input is updated by computing the dot product between the input matrix and the weights matrix plus a bias term. In each Ramp layer, the input is discarded if negative and accepted if positive.

Here is an illustration of how linear function and activation function works.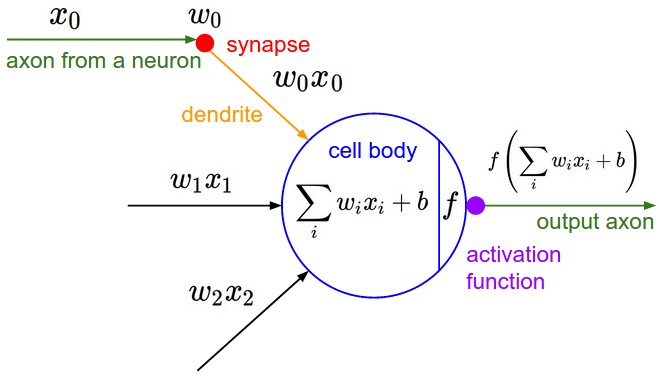

Into the Network

The dataset for training and testing is generated by randomly selecting 2 lists of 10000 integers from 1 to 2048(which ranges from the 0th to the 11th power of 2) as the input, with their sum(product) as the output. For each input element in the list, we first transform it into a list of its binary representation, then reverse it(the neural net reads the list from right to left) and pad zeros to the right so that all inputs are of the same size.

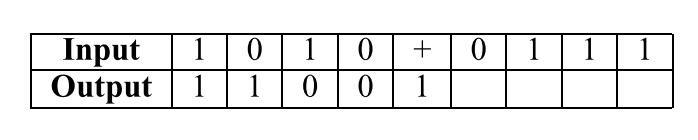
Here is an example of how addition works

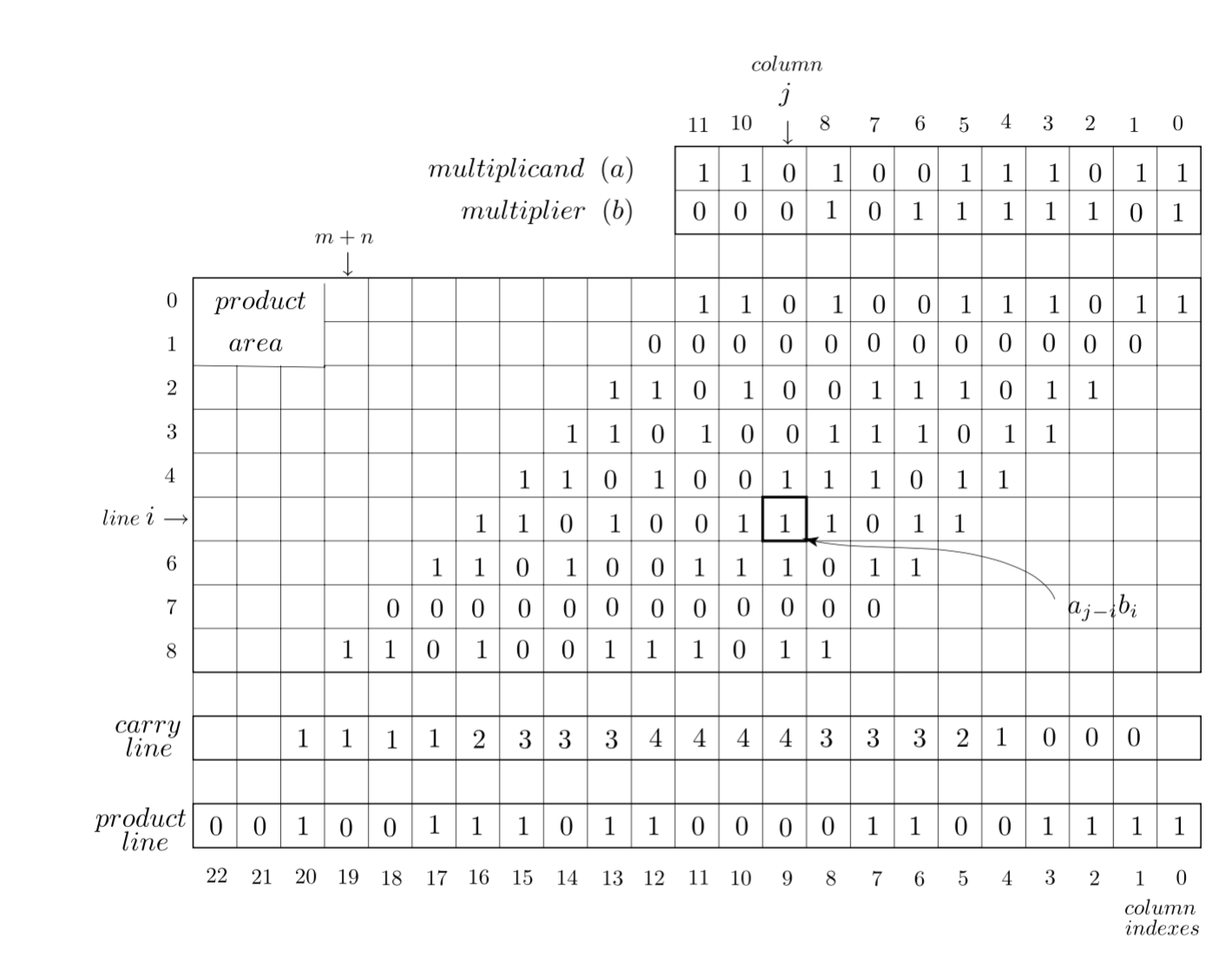
This is how multiplication works

Codes for the generation of the dataset

int1 = RandomInteger[2048]
int2 = RandomInteger[2048]
x1 = PadRight[Reverse[IntegerDigits[int1, 2]], 12]
x2 = PadRight[Reverse[IntegerDigits[int2, 2]], 12]
sum = PadRight[Reverse[IntegerDigits[int1 + int2, 2]], 12]
product = PadRight[Reverse[IntegerDigits[int1*int2, 2]], 24]

Note: 80% of the dataset is the training set, while 80% of the training set is the validation set. The rest of the dataset is the test set.

Because the size of output layer must match the size of output tensor, the number of neurons in the last two layers(one linear layer and one activation layer) is fixed(12 for add task, 24 for multiplication task). In other layers, we vary the number of neurons from 12 to 32, with the step of 4, so that there are 6 possible configurations for a single linear layer. Because activation layer performs element-wise operation on the previous layer, the number of neurons is the same as the previous layer. To sum up, from 4-layer network to 10-layer network, I tried 6+36+216+1296=1554) different networks, with a batch size of 50 and an ADAM Optimizer.

After training each network on the training set, I test them on the test set and record the mean squared loss to a list. I plot the residual of each network on both addition task and multiplication task. In the graphs below, each point on the plane represents a specific network, with the vertical axis represents the mean squared loss value.

Loss of Addition Task

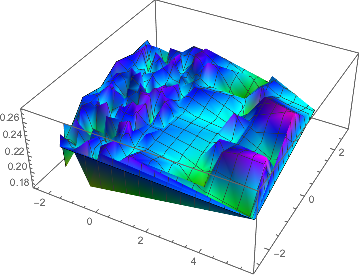
Loss of Multiplication Task

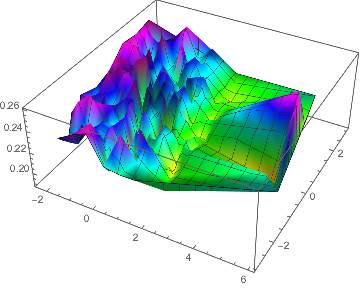
Best Networks So Far

Here is a map of the architecture of the best 50 networks on addition task with respect to its loss. Note: Each element of the list represents the number of neurons in the layer of the same index as the element. Zero means the layer doesn't exist. For example, {12,12,12,12,0,0,0,0,0,0} represents a 4-layer network with 12 neurons in all its layers.

{24,24,28,28,32,32,12,12,0,0}->0.181261,{32,32,24,24,12,12,0,0,0,0}->0.184372,{32,32,16,16,16,16,32,32,12,12}->0.186459,{32,32,24,24,28,28,12,12,0,0}->0.188729,{28,28,24,24,28,28,12,12,0,0}->0.190486,{32,32,20,20,32,32,28,28,12,12}->0.190782,{24,24,28,28,20,20,20,20,12,12}->0.191165,{20,20,20,20,32,32,32,32,12,12}->0.191548,{28,28,28,28,28,28,28,28,12,12}->0.191761,{24,24,16,16,28,28,12,12,0,0}->0.192015,{28,28,20,20,28,28,32,32,12,12}->0.192752,{24,24,32,32,32,32,12,12,0,0}->0.192777,{32,32,24,24,32,32,28,28,12,12}->0.193613,{16,16,20,20,20,20,12,12,0,0}->0.193732,{32,32,20,20,32,32,24,24,12,12}->0.19423,{20,20,32,32,28,28,28,28,12,12}->0.194303,{20,20,16,16,24,24,32,32,12,12}->0.195255,{20,20,12,12,28,28,28,28,12,12}->0.195482,{28,28,28,28,16,16,24,24,12,12}->0.195776,{24,24,32,32,12,12,20,20,12,12}->0.195925,{28,28,32,32,32,32,28,28,12,12}->0.196085,{32,32,32,32,28,28,24,24,12,12}->0.196094,{20,20,32,32,32,32,24,24,12,12}->0.196312,{20,20,12,12,28,28,32,32,12,12}->0.19672,{28,28,16,16,20,20,32,32,12,12}->0.196777,{20,20,12,12,16,16,28,28,12,12}->0.197219,{16,16,16,16,24,24,24,24,12,12}->0.197219,{12,12,20,20,20,20,16,16,12,12}->0.197522,{32,32,16,16,28,28,12,12,0,0}->0.197642,{32,32,12,12,0,0,0,0,0,0}->0.197812,{28,28,32,32,12,12,0,0,0,0}->0.198006,{32,32,16,16,20,20,32,32,12,12}->0.198121,{24,24,20,20,32,32,28,28,12,12}->0.198123,{16,16,20,20,28,28,28,28,12,12}->0.198647,{16,16,24,24,12,12,0,0,0,0}->0.198828,{24,24,16,16,24,24,28,28,12,12}->0.198953,{32,32,24,24,24,24,12,12,0,0}->0.198963,{32,32,28,28,24,24,28,28,12,12}->0.199014,{24,24,20,20,16,16,20,20,12,12}->0.199069,{28,28,16,16,20,20,20,20,12,12}->0.199158,{12,12,28,28,32,32,12,12,0,0}->0.199186,{16,16,20,20,24,24,32,32,12,12}->0.199247,{12,12,12,12,20,20,12,12,0,0}->0.199263,{28,28,32,32,12,12,32,32,12,12}->0.199339,{20,20,24,24,28,28,32,32,12,12}->0.199442,{16,16,16,16,12,12,28,28,12,12}->0.199506,{12,12,12,12,20,20,32,32,12,12}->0.199613,{28,28,20,20,32,32,12,12,0,0}->0.199742,{16,16,20,20,24,24,16,16,12,12}->0.199752,{20,20,20,20,32,32,12,12,0,0}->0.199797

Best Networks on Multiplication Task

{12,12,28,28,28,28,12,12,24,24}->0.188287,{24,24,32,32,32,32,24,24,0,0}->0.190111,{12,12,24,24,12,12,16,16,24,24}->0.19261,{32,32,28,28,32,32,24,24,0,0}->0.192898,{20,20,16,16,24,24,24,24,24,24}->0.192993,{24,24,24,24,12,12,12,12,24,24}->0.193376,{16,16,16,16,16,16,16,16,24,24}->0.193589,{32,32,12,12,32,32,24,24,0,0}->0.193781,{16,16,24,24,16,16,12,12,24,24}->0.19458,{28,28,20,20,28,28,24,24,0,0}->0.194658,{16,16,16,16,24,24,24,24,0,0}->0.194702,{24,24,20,20,28,28,24,24,0,0}->0.195123,{12,12,28,28,24,24,0,0,0,0}->0.195287,{20,20,28,28,28,28,24,24,0,0}->0.195321,{32,32,16,16,28,28,24,24,0,0}->0.195372,{12,12,20,20,12,12,16,16,24,24}->0.195441,{20,20,16,16,24,24,24,24,0,0}->0.195517,{24,24,24,24,28,28,24,24,0,0}->0.195627,{20,20,24,24,24,24,0,0,0,0}->0.195645,{24,24,20,20,32,32,24,24,0,0}->0.195777,{12,12,24,24,12,12,20,20,24,24}->0.196058,{28,28,32,32,24,24,24,24,0,0}->0.196079,{24,24,12,12,16,16,16,16,24,24}->0.196131,{28,28,28,28,32,32,24,24,0,0}->0.196503,{20,20,20,20,32,32,24,24,0,0}->0.1967,{24,24,28,28,20,20,12,12,24,24}->0.197083,{28,28,20,20,32,32,24,24,0,0}->0.197127,{28,28,24,24,24,24,0,0,0,0}->0.197172,{24,24,32,32,16,16,16,16,24,24}->0.19731,{16,16,24,24,24,24,0,0,0,0}->0.197401,{24,24,32,32,24,24,0,0,0,0}->0.197452,{16,16,20,20,24,24,0,0,0,0}->0.197596,{16,16,16,16,28,28,20,20,24,24}->0.197604,{20,20,12,12,32,32,24,24,24,24}->0.197753,{24,24,24,24,32,32,24,24,0,0}->0.197809,{16,16,12,12,12,12,16,16,24,24}->0.197913,{12,12,12,12,16,16,20,20,24,24}->0.197922,{24,24,24,24,20,20,24,24,0,0}->0.197984,{20,20,24,24,28,28,24,24,0,0}->0.198084,{24,24,32,32,24,24,24,24,0,0}->0.198089,{28,28,28,28,28,28,24,24,0,0}->0.19811,{24,24,12,12,12,12,20,20,24,24}->0.19814,{28,28,32,32,32,32,24,24,0,0}->0.198326,{16,16,20,20,32,32,24,24,0,0}->0.198511,{24,24,32,32,16,16,12,12,24,24}->0.198548,{16,16,28,28,24,24,12,12,24,24}->0.198605,{32,32,24,24,32,32,24,24,0,0}->0.198641,{16,16,32,32,28,28,24,24,0,0}->0.19874,{20,20,16,16,32,32,24,24,0,0}->0.198799,{32,32,32,32,28,28,24,24,0,0}->0.198839

Conclusion

Although there isn't a clear pattern of how the architecture of the neural network relates to its performance, there's still something we can conclude from the experiment: Greater depth and width of network don't necessarily result in better performance. The accuracy of a network performing arithmetic operations is decided by multiple factors. According to the recorded data, it seems networks of reasonably numerous layers, a gradual increase in number of neurons in each layer, and fully connectivity of neurons yield the best result. Nonetheless, more work need to be done to fully grasp the philosophy behind the best models in the experiment.