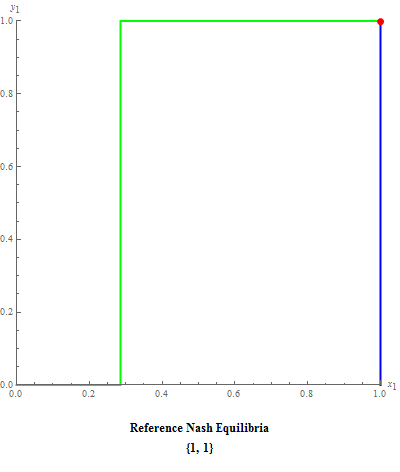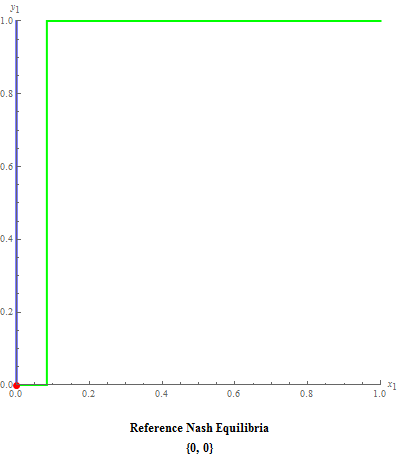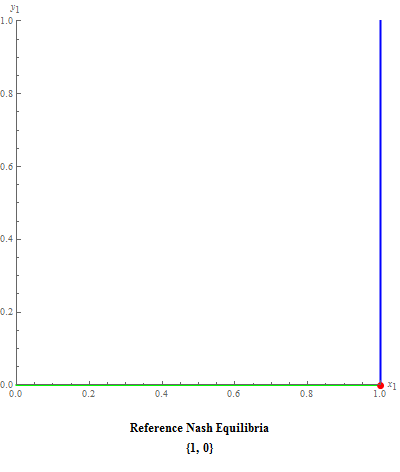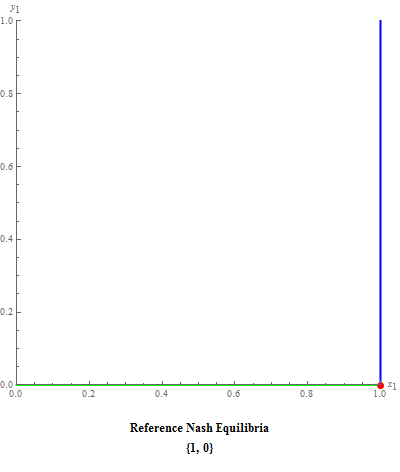
A first version of a program that finds Nash equilibrium sets in dyadic mixed strategy games was published earlier in the Wolfram Demonstrations Project. That code may be freely viewed, verified and downloaded from the site. We developed a new one, to exclude slow execution of the published version, and publish this post to ask help of the Wolfram Community on it improving...

We also want to ask community opinions about theorem proving with means of pieces of Wolfram language codes...

Dyadic two-person mixed strategy games form the simplest case for which we can determine all the possible types of Nash equilibrium sets. The set of Nash equilibria in a particular game is determined as an intersection of graphs of optimal reaction mappings of the first and the second players. We define a function that gives directly as its values the Nash equilibrium set corresponding to the values of payoff matrices. Totally, the function has $36$ values, i.e. $36$ distinct sets of Nash equilibria. To give an expedient form to such a function definition, we use a program written in the Wolfram language.

Game statement and its simplification

The dyadic two-player mixed strategy game is defined by the tuple

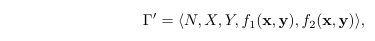
where

• $N=\{1,2\}$ is a set of players,
• $X=\{{\bf x}\in \mathbb{R}^2: x_1+x_2=1, x_1\geq 0, x_2\geq 0\}$ is a set of strategies of the first player,
• $Y=\{{\bf y}\in \mathbb{R}^2: y_1+y_2=1, y_1\geq 0, y_2\geq 0\}$ is a set of strategies of the second player,
• $f_i:X\times Y\rightarrow R$ is a player's $i\in N$ payoff function,
• $f_1({\bf x,y})={\bf x}^T A {\bf y}$, $A\in \mathbb{R}^{2\times 2},$
• $f_2({\bf x,y})={\bf x^T} B {\bf y}$, $B\in \mathbb{R}^{2\times 2}.$

So,

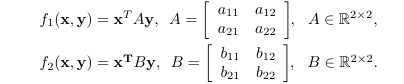
We suppose that every player maximizes the value of his payoff function.

Remark, the strategy set for each player is a segment --- a hypotenuse of the correspondent unit simplex (right triangle) in $\mathbb{R}^2$.

We can reduce game $\Gamma^\prime$ to a simpler game $\Gamma$ by substitutions:

• $x_1=x, x_2=1-x, 0\leq x\leq 1,$
• $y_1=y, y_2=1-y, 0\leq y\leq 1.$

So, in $\Gamma$ players have as strategy sets segment $[0,1]$ and as payoff functions:

• $f_1(x,y)=\left(\alpha y + \alpha_0\right) x + \left(a_{21}-a_{22}\right) y + a_{22},$
• $f_2(x,y)=\left(\beta x + \beta_0\right) y + \left(b_{21}-b_{22}\right) x + b_{22},$

where

• $\alpha = a_{11}-a_{21}+a_{22}-a_{12}, \alpha_0 = a_{12} - a_{22}-,$
• $\beta = b_{11}-b_{12}+b_{22}-b_{21},\, \beta_0 = b_{21} - b_{22}.$

Remark. As the first player chooses the value of variable $x$ and the second --- of variable $y$, to compute their optimal strategies the players can omit the last two members of their payoff functions. So, they can solve a simplified game:

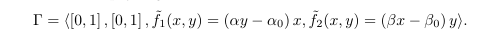
Proposition. The games $\Gamma^\prime$ and $\Gamma$ are equivalent.

Further, we will use as $\Gamma^\prime$, as $\Gamma$ to construct the sets of Nash equilibria.

Optimal Value Functions and Best Response Mappings

The game $\Gamma$ represents a game on a unit square. The payoff functions are bilinear, i.e. for a fixed value of one variable, the functions become linear functions in relation to the other variable. To choose his best strategy, the correspondent player must solve a parametric linear programming problem on a unit segment.

For any player we can define the optimal value function and the best response mapping:

$\varphi_1(y) = {\displaystyle\max_{x\in [0,1]} f_1(x,y)}$ - optimal value function of the first player,

$\gamma_1(y) = {\displaystyle{\rm Arg}\max_{x\in [0,1]} f_1(x,y) }={ \displaystyle{\rm Arg}\max_{x\in [0,1]} \tilde f_1(x,y)}$ - best response mapping of the first player,

$\varphi_2(x) ={ \displaystyle\max_{y\in [0,1]} f_1(x,y)}$ - optimal value function of the second player,

$\gamma_2(x) ={ \displaystyle{\rm Arg}\max_{y\in [0,1]} f_2(x,y)} = {\displaystyle{\rm Arg}\max_{y\in [0,1]} \tilde f_2(x,y)}$ - best response mapping of the second player.

To determine Nash equilibrium sets, we need the graphs of best response mappings:

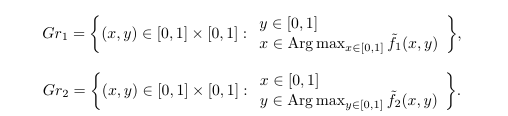
These graphs are functions of payoff matrices $A$ and $B$. Evidently,

$$NE = Gr_1\bigcap Gr_2. $$

Now, let us consider the problem of constructing the Nash equilibrium set as a function of the payoff matrices $A$ and $B$, i.e. let us consider the problem of constructing analytically the Nash equilibrium set. In this context, let us consider the graphs as the functions of $\alpha, \alpha_0$ and $\beta, \beta_0$.

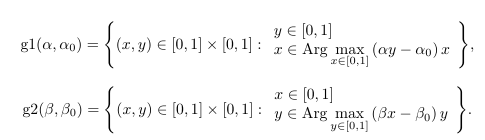
Optimal solutions of the optimization problems in the expressions for ${{\rm g1}(\alpha,\alpha_0)}$ and ${{\rm g2}(\beta, \beta_0)}$ are attained either on one of extremities, or on the whole segment $[0,1]$. As the result depends of both the values of ${\rm g1}(\alpha,\alpha_0)$ and ${\rm g2}(\beta, \beta_0)$, we can now establish exact expressions for these graphs.

The graph of best response mapping of the first player is:

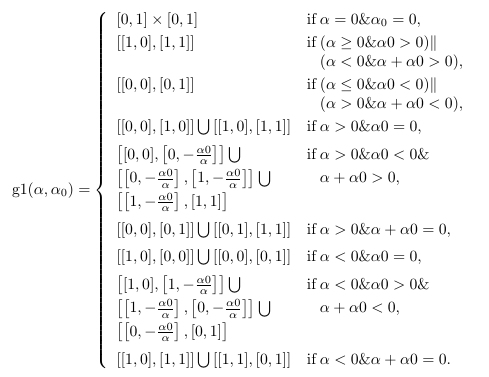
Remark. Above, we denoted the unit square by $[0,1] \times [0,1]$ and the segment which connects two points, e.g. $[0,0]$ and $[1,0]$, by an expression of the type $\left[ [0,0], [1,0] \right]$.

Remark. From the expression for ${\rm g1}(\alpha,\alpha_0)$ we can conclude that its values may be:

1. a unit square,
2. a unit segment,
3. a reunion of two connected segments on the boundary of the unit square (one horizontal and one vertical),
4. a reunion of three connected segments (two vertical, on the opposite vertical sides of the unit square, connected by the third interior horizontal segment, from one lateral side to the other).

It is important to observe that the condition specified by the concrete values of $\alpha $ and $\alpha 0$ corresponds to an entire class of matrices $A\in \mathbb{R}^{2\times 2}$. More the more, accordingly to the expressions that define $\alpha$ and $\alpha_0$, the function ${\rm g1}(\alpha,\alpha_0)$ is defined on entire space $\mathbb{R}^{2\times 2}$, i.e. it is defined for any numeric dyadic matrix $A$.

The graph of best response mapping of the second player is:

For ${\rm g2}(\beta,\beta_0)$ analogical conclusions are valid, as for ${\rm g1}(\alpha,\alpha_0)$.

Nash equilibria

As every graph of best response mapping has 9 different possible forms for particular instances of payoff matrices $A$ and $B$, their intersection abstractly may generate 81 possible instances/cases of Nash equilibrium sets. Some of them coincide.

Theorem. Nash equilibrium set in dyadic mixed strategy games may have 36 distinct instances/cases.

Proof. The proof is constructive. It enumerates the distinct possible cases in a form of Wolfram language program.

First, the best response mapping graphs are defined as the Wolfram language functions.

Second, the Nash equilibrium set is defined as the Wolfram language function too.

At the last, we present a Wolfram language code to manipulate all elements together and to highlight results for different initial data.

As the enumerated 36 cases include all the 81 abstractly possible cases of the results of graph intersections, the proof is complete. $\square$

Even though we establish 36 different forms/cases for Nash equilibrium set, we can summarize them and can conclude that Nash equilibrium set may be:

• a border point as one of the vertices of the square (see cases: 10, 11, 13, 14),
• an interior point of the square (see cases: 5, 23),
• two border points as two opposite vertices of the square (see cases: 15, 29),
• a unit border segment as one of the sides of the square (see cases: 2, 3, 9, 12),
• two unit border segments as two connected sides of the square (one vertical and one horizontal) (see cases: 4, 6, 7, 8),
• a reunion of one point and one non-unit segment as one vertex of the square and one non-unit segment on opposite side of the square (see cases: 16, 19, 21, 25, 28, 32, 34, 36),
• one non-unit segment as a segment on one of the sides of the square (see cases: 17, 22, 24, 26, 27, 30, 31, 35),
• a graph of one of the players as a reunion of three connected segments (see case 18),
• three distinct points as two corner opposite vertices of the square and one interior point (see cases: 20, 33),
• a unit square (see case 1).

An example of snapshot:

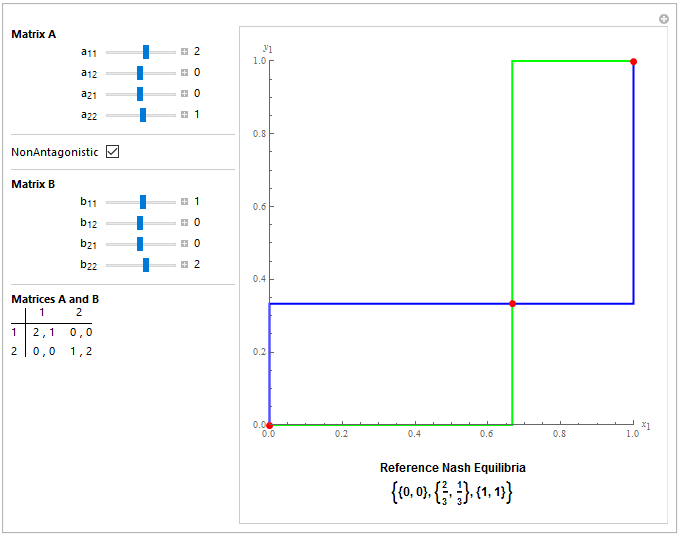
Corollary. Nash equilibrium set in dyadic mixed strategy games may be formed by

• a point,

• two points,

• three points,

• a segment,

• two connected segments,

• three connected segments,

• reunion of non-connected one point and one segment,

• the unit square.

Conclusions

For dyadic mixed strategy games we exposed a Wolfram language program and its theoretical reasons. The program permits to construct and visualize the Nash equilibrium set as a function of matrices $A$ and $B$.

An earlier version of this program "Set of Nash Equilibria in 2x2 Mixed Extended Games" was published in the Wolfram Demonstrations Project. That code may be freely viewed, verified and downloaded from the site. We developed a new version to exclude slow execution in the first version.

We ask Wolfram Community opinions and ideas: may be this code essentially shortened and simplified ?

Bibiliography

1. Ungureanu, V. Nash equilibrium set function in dyadic mixed-strategy games, Computer Science Journal of Moldova, Vol.~25, No.~1 (73), 2017, pp. 3--20.

The demonstration is attached.

Attachments:

ne2x2.nb