Surely, it is mutually assumed that your parameters f, g, y, are numeric and fixed. To solve symbolically your problems is difficult. So, I propose to define your functions as it follows:

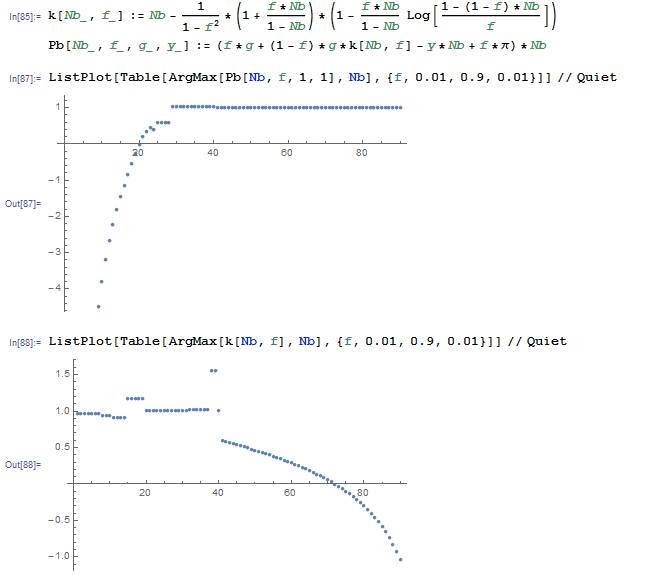
k[Nb_, f_] := 
 Nb - 1/(1 - 
    f^2)*(1 + (f*Nb)/(
     1 - Nb))*(1 - (f*Nb)/(1 - Nb) Log[(1 - (1 - f)*Nb)/f])
Pb[Nb_, f_, g_, y_] := (f*g + (1 - f)*g*k[Nb, f] - y*Nb + f*\[Pi])*Nb

It must be observed that in definition there is Log function... Right conclusions must be done... By fixing values of g=1 and y=1, we can tabulate the value of f and solve corespondent optimization problems. The results we can visualize by applying ListPlot:

ListPlot[Table[
   ArgMax[Pb[Nb, f, 1, 1], Nb], {f, 0.01, 0.9, 0.01}]] // Quiet

We can do the same thing for the function k[]:

ListPlot[Table[ArgMax[k[Nb, f], Nb], {f, 0.01, 0.9, 0.01}]] // Quiet

Evidently, now you have tools for doing your tests and continuing your research.

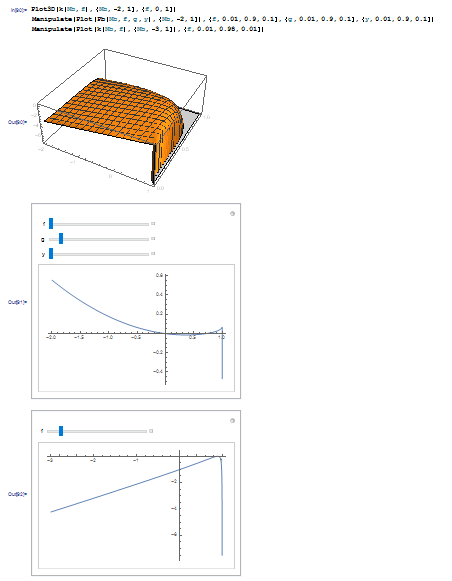
Additionally, you can analyze function graphs by their plots and manipulations:

Plot3D[k[Nb, f], {Nb, -2, 1}, {f, 0, 1}]
Manipulate[
 Plot[Pb[Nb, f, g, y], {Nb, -2, 1}], {f, 0.01, 0.9, 0.1}, {g, 0.01, 
  0.9, 0.1}, {y, 0.01, 0.9, 0.1}]
Manipulate[Plot[k[Nb, f], {Nb, -3, 1}], {f, 0.01, 0.98, 0.01}]