Basically, I want to be able to play around with sets and discrete mathematics in Wolfram, and it's pretty important that at least when it comes to displaying results that the notation is formal. I've learned TraditionalForm[] can be quite useful. I really just want to use Wolfram to do math for class.
E = { 2n : 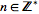 }
}
In a more generalized form I just want to be able to say E = {Expression:Condition}
Then I want to be able to do three things.
Either specify a specific variable that I know satisfies the condition and then evaluate the expression for the given condition. Such as n=5 because I know that 5 is a member of Z*, and then get the output of 10. The problem with this is that discovering whether some variables meet a complex condition can require a high amount of computation.
In that case, I want to be able to generate a variable that meets the stated condition. I want to be able to generate a variable, or the set of variables that meets the stated condition. I know it is more complicated in this case because Z* is an infinite set, but I would put additional constraints on variable generation such as <10000 for practical purposes.
Imagine that the statement was
E= 2n such that n is a member of the members that satisfy y^2=4
Sorry, my math skills are actually not that great -- that's why I'm working on them -- so I don't even know how to represent this statement formally, but I hope I'm getting my point across. This means that I would like wolfram to be able to discover that 2 and -2 satisfy the condition, and then evaluate E for each case and output for this expression 4 and -4.
I don't expect to be handed a bunch of code, but I do understand many fundamental programming principles. Wolfram is certainly quite different, so I've tried not to approach it in the traditional way, and I have tried to "forget" the ways that most traditional programming languages work; it seems I might have been a bit too hasty in that regard. But hopefully someone can point me in the right direction.
It would also be very helpful to evaluate the expression for say the first 10 variables that meet the condition and then store the results to an array. For example, in the case of the original question, evaluate E for the first 10 integers of the set of all positive integers.The result would be evaluation of 2n for {1, 2, 3, ...,10} and subsequently, I would like to store the results in an array that would be {2, 4, 6, ..., 20}
If you could also point me to a place that described infinite list generation so you do not have to spend time on it yourself that would be great. I don't want to waste your time.
Thanks for your response and taking the time to help!