Abstract

Often, the voice of a person through a microphone is not well understandable because of the external noise. The goal of this project is to intelligently remove the interference of the noise that appears through a microphone. To achieve the intelligent noise cancellation we dynamically distinguish and remove the "noisy" regions in the sound spectrogram with respect to different parameters.

Introduction

Audio File is a wave which represents different frequency waves' overlay. Fourier transformation was applied in order to get the structure in frequency range. By the Fourier transformation we got frequency characteristic of noise. Then a model was applied supposing that the noise amplitude is small, and to remove it exponential cut offs can be used. The experiment showed that partitioning the audio with a factor, applying th changes and composing the audio back is faster than performing the changes on the original audio. The finally result is the Audio data with reasonably less noise.

Below we describe the code ___

Check for proper audio and extract "SampleRate", "Length" and "Type".

getAudioMeasurements[a_] := 
   Module[{sr, t, l, err = None},
      If[!AudioQ[a], err = generateError[a]];
      If[err =!= None, Return[err]];

      (*Extract the sample rate and set to 44100 if the extraction was not successful*)
      sr = AudioMeasurements[a, "SampleRate"];
      If[!IntegerQ[sr], err=generateError[a]]; (*If the samplerate is not an integer it is not a valid audio*)

      (*Extract the sample rate and set to Real32 if the extraction was not successful*)
      t = AudioMeasurements[a, "Type"];
      If[!MatchQ[t, supportedAudioTypes], err=generateError[a]];(*If the type is not an one of the supperted ones it is not a valid audio*)

      (*Extract the length of an audio and return $Failed if the extraction was not successful*)
      l=AudioMeasurements[a, "Length"];
      If[!IntegerQ[l], generateError[a]];

      {sr, t, l}
    ]

Compute the window size(wSize) and offset(getOffset) If wSize and/or getOffset are not given, they are being calculated with respect to well known factors .

getWindowSize[wSize_, sr_] := 
   With[{wTime = 2048./44100}, 
      If[wSize === Automatic, Round[wTime * sr], wSize]
    ]
getOffset[wSize_, offsetGiven_] := 
   With[{ratio = .25},
      If[offsetGiven === Automatic, Round[wSize * ratio], offsetGiven]
    ]

Here we import exponential function which cuts off the frequencies that are below or above the mean frequency value.Joining matrix with conjugate matrix exempt from imagination part.As a result of transformation the result of inverse Fourier is not changing.But the result of counting value is changing.

expfunc[aa_,thresh_]:=Map[If[Abs[#]>=thresh,#,#*Exp[1-(thresh/(Abs[#]+0.01*thresh))^4]] &, aa];
separateSpectArray[array_, thresh_] := Map[expfunc[-(thresh/(Abs[#]+0.01*thresh))^2] &, array]

After the changes in spectrogram we return to the audio data via using Inverse Fourier transformation.

conjugateTwoPartsSpectArray := Compile[{array, offset, win, wSize, l},
   Module[{res={}, concat}, 
      concat = Developer`ToPackedArray[Join[array,Take[Conjugate[Reverse[array,{2}]], All, {If[EvenQ[wSize], 2, 1, 2], -2}], 2]];
      res = ConstantArray[0., wSize + Ceiling[l]];
      ParallelDo[res[[1 + (i-1)*offset ;; (i-1)*offset + wSize]] += Re[InverseFourier[concat[[i]], FourierParameters->{1,-1}]]*win,
         {i, Range[Length[concat]]}
       ];                                                                              
      res
    ]]

Use given Function to remove noise

Denoise function divide audio file into several parts and apply Denoise part function on the every part. Our process perform the following operations:

• 1.Calculate Spectrogram of audio file with Fourier transformation

• 2.Apply Exponential cut offs

• 3.Get audio file from spectrogram using Inverse Fourier

In order to calculate the size of the window HannWindow function is used as default window. The advantage of the Hann window has very low aliasing. The Hann function is typically used as a window function in digital signal processing to select samples series subset in order to perform a Fourier transform or other calculations.

$$\begin{cases} \alpha +\alpha (-\cos (2 \pi x))+\cos (2 \pi x) & -\frac{1}{2}\leq x\leq \frac{1}{2} \\ 0 & \text{True} \end{cases}$$

denoisePart[audio_, wType_:HannWindow, wSizeGiven_:Automatic, offsetGiven_:Automatic, testFunction_:False]:= 
   Module[{l, sr, t, win=wType,  wSize, offset, averThresh, spectArraySep, spectArraySepModify, spectArray,spectArrayModify,  result},
      With[{err = getAudioMeasurements[audio]}, If[err === $Failed, Return[err], {sr, t, l} = err]];          
         wSize = Quiet@getWindowSize[wSizeGiven, sr];
         offset = Quiet@getOffset[wSize, offsetGiven];
         win = Quiet@generateWindow[win, wSize]];

Then we used SpectrogramArray to get its spectrogram in an array form

    spectArray = Quiet@Developer`ToPackedArray[SpectrogramArray[audio,wSize,offset,win]]

After that calculate main square value of argument with average threshold is computed

If[!testFunction,
            averThresh = Quiet@computeAverageThreshold[spectArray[[All, 1 ;; Floor[wSize/2 + 1]]]];
            spectArraySep = Quiet@separateSpectArray[spectArray[[All, 1 ;; Floor[wSize/2 + 1]]], averThresh];
            spectArraySepModify = Quiet@Map[# &, spectArraySep, {2}]
            ,
            spectArraySepModify = spectArray[[All, 1 ;; Floor[wSize/2 + 1]]]
          ];

Then we apply inverse Fourier to got the data of audio from Spectrogram

spectArrayModify = Quiet@conjugateTwoPartsSpectArray[spectArraySepModify, offset, win, wSize, l];

Finally, We got our results

result = Developer`ToPackedArray[Take[spectArrayModify, l] / (Total[win^2] / offset)];
         result = Audio[result, If[t ==="Real", "Real", "Real32"], SampleRate->sr];

         If[!AudioQ[result], Return[$Failed]];

         result

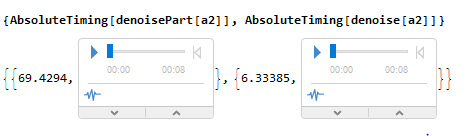
We also use palatalization functions to make faster denoise process.

An optimal factor is calculated during the experiments, which allows to partition the audio in such parts, so that denoising process is fastest.

One can specify all the parameters for the denoising function, though it works in optimal way with defaults values.

denoise[audio_, secondsInPartitions_:Automatic, wType_:HannWindow, wSizeGiven_:Automatic, offsetGiven_:Automatic, testFunction_:False]:=      
           Module[{audioList, optFactor = 3.9508808651665794`, optSecondsInPartitions, d, useOpt = True},
                 If[!AudioQ[audio], Return[$Failed]];

                 d = AudioMeasurements[audio, "Duration"]; 
                 optSecondsInPartitions = (d * 1.0)/optFactor;  

                 useOpt = If[Internal`RealValuedNumericQ[secondsInPartitions] && secondsInPartitions > 0 && secondsInPartitions < d, False, True];

                 audioList = AudioPartition[audio, If[useOpt, optSecondsInPartitions, secondsInPartitions]];
                 AudioTrim[AudioJoin[ParallelMap[denoisePart[#, wType, wSizeGiven, offsetGiven, testFunction]&,audioList]]]
            ]    

        denoise[audio_, OptionsPattern[]] := denoise[audio, OptionValue[SecondsInPartition], HannWindow, Automatic, Automatic, False]

Attachments: