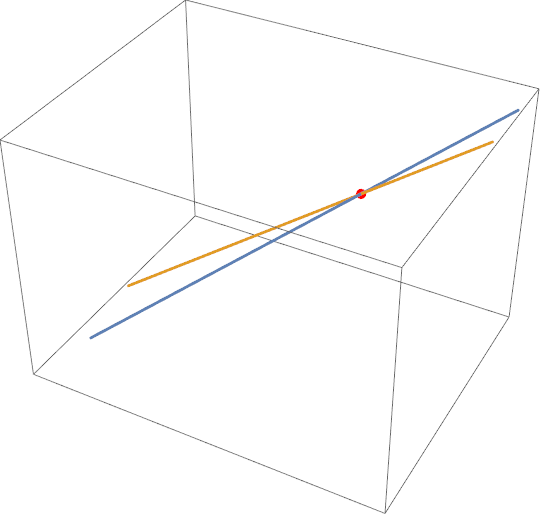
Here is another approach. Lines are defined by vector equations. The vector equation for each line is derived from a pair of points on the line, but they are just two points on the line -- it is not a line segment with endpoints. We then have two lines, each parameterized by its own parameter. FindInstance is used to determine a pair of parameter values for which the lines share a common point. If no intersection exists, it will return an empty list.
(* a vector equation for a line from two points *)
pa1 = {-2, -3, -1}; pa2 = {3, 2, 2};
lineA[t_] := pa1 + t Normalize[pa2 - pa1]
(* a second line *)
(* notice they intersect at {3,2,2} *)
pb1 = {-4, 1, -3}; pb2 = {3, 2, 2};
lineB[t_] := pb1 + t Normalize[pb2 - pb1]
(* find an intersection *)
(* if they don't intersect, FindInstance would return { } *)
intersection = FindInstance[lineA[t1] == lineB[t2], {t1, t2}]
{{t1 -> Sqrt[59], t2 -> 5 Sqrt[3]}}
Show[Graphics3D[{PointSize[Large], Red,
Point[lineA[t1] /. intersection[[1]]]}],
ParametricPlot3D[{lineA[t], lineB[t]}, {t, -5, 15}]]