NOTE: All utility functions are defined at the end and also in the attached notebook.
You can compute the first million digits of $\pi$ without printing them in < 1 second (the 1st number in the the time of computation without printing, and the printed later image is actually only a minuscule part of the whole 10^6 digits):
tim[N[Pi, 10^6]]
0.314149, 0

and then print the last 99:
tim[Mod[Round[10^10^6*%], 10^99]]
0.021651,0
315614033321272849194418437150696552087542450598956787961303311646283996346460422090106105779458151
Far better than digits is a continued fraction:
longer[Pi, 9]

This expression = $\pi$
Simplify[ReleaseHold[%]]
?
and can be freely lengthened (or shortened):
longer[%%]

Notice that $e$, unlike $\pi$, has a pattern:
longer[E, 9]
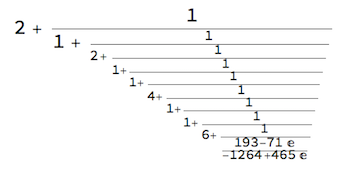
But proving that ? will never develop a pattern is one of the great unsolved problems. For faster, but non-resumable continued fractions, Mathematica has, e.g.,
ContinuedFraction[Pi, 9]
{3, 7, 15, 1, 292, 1, 1, 1, 2}
Note the largish term at position 431:
Take[ContinuedFraction[Pi, 433], -4]
{1, 4, 20776, 1}
Around 1986, in a calculation taking several weeks, I found
tim[Take[ContinuedFraction[Pi, 11504932], -4]]
8.36905,4
{1, 1, 878783625, 6}
I thought Eric Weisstein found a bigger one, but Pi Continued Fraction page doesn't seem to say. Simple functions of e also have patterns:
longer[(E^2 + 1)/(E^2 - 1), 9]

$e^x$ has a nice infinite series:
SeriesCoefficient[E^x, {x, 0, n}]

This means
(#1 == Activate[#1] & )[Inactive[Sum][x^n/n!, {n, 0, Infinity}]]
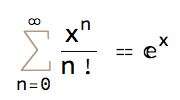
Taking a few terms
ser = Activate[%[[1]] /. Infinity -> 9]
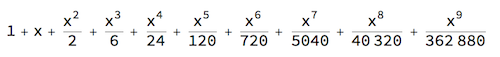
we can numerically test Euler's celebrated
(#1 == Activate[#1] & )[E^Inactivate[I*Pi]]
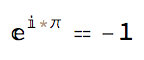
N[ser /. x -> I*Pi]
-0.976022 + 0.00692527 I
The square root of Euler's identity is
(#1 == Activate[#1] & )[E^(Inactivate[I*Pi]/2)]
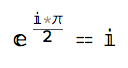
N[ser /. x -> I*(Pi/2)]
0.0000247373 + 1. I
We can even use Euler's identity to calculate ? by solving
eq = E^(I*x) + 1 == 0
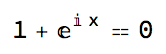
This has infinitely many solutions!
Simplify[Solve[eq]]
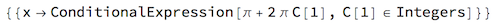
Unprotect[C]; Table[%[[1, 1]], {C[1], -2, 2}]
{x -> -3 ?, x -> -?, x -> ?, x -> 3 ?, x -> 5 ?}
Newton's iteration says: to solve $f(x)=0$, choose an initial guess for x and iterate $g(g(...g(x)))$ where $g = x - f/ df/dx$
g[x] = Simplify[x - eq[[1]]/D[eq[[1]], x]]
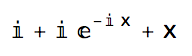
Starting with a very precise value of 3
NestList[I/E^(I*#1) + #1 + I & , 3.`69., 7]

Each iteration of Newton's method typically doubles the number of correct digits. But isn't it slightly cockeyed to seek a real answer by applying a complex function to a real approximation? Suppose we just took the real part of $g$:
ComplexExpand[Re[g[x]]]
x + Sin[x]
(Remembering that Euler's identity generalizes to Euler's formula:)
(#1 == ComplexExpand[#1] & )[E^(I*x)]
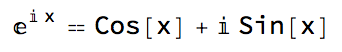
Using this new $g$
NestList[#1 + Sin[#1] & , 3.`69., 5]

triples the accuracy each time! What if we start with 9 instead of 3?
NestList[#1 + Sin[#1] & , 9.`69., 5]

Dividing the last approximation by 3
Last[%]/3
3.1415926535897932384626433832795028841971693993751058209749445923078
Utility functions
These are definitions of all utility functions you will need for the above evaluations.
Clear[tim];
tim[xp_]:=(Print[#[[1]],",",Length[#[[2]]]];
If[#[[1]]>69,Speak[#[[1]]]];#[[2]])&@AbsoluteTiming[xp]
SetAttributes[tim,HoldAll]
Clear[shorter];
shorter[cf_,0]:=cf
shorter[cf_,n_: 1]:=shorter[cf/.(a_: 0)+1/HoldForm[r_]:>HoldForm@@{(a+1/r)},n-1]
Clear[longer];
longer[cf_,0]:=cf
longer[x_?NumericQ,n_: 1]:=longer[HoldForm@@{x},n]
longer[cf_,n_: 1]:=longer[cf/.HoldForm[r:Except[_Integer]]:>
Floor[r]+1/HoldForm@@{Simplify@Together[1/Mod[r,1]]},n-1]
tail[cf_]:=Cases[cf,HoldForm[x_]->x,\[Infinity]][[1]]
 Attachments:
Attachments: