Introduction:
On Wednesday October 18, 2016, I had the honor of co-presenting the findings of probabilistic CA at the 2016 Wolfram Technology Conference. Posted here is notebook (.nb) file that contains the demonstration from my talk. I am very interested in CA, and I believe this application that I created can shed some light on the overall structure of the CA space. This project borrows code (with permission) from the work of Dr. Rodrigo Obando, Columbus State University. He was the co-presenter with me at the conference. His code combined with my own produces what we believe is true probabilistic cellular automata.
Overview:
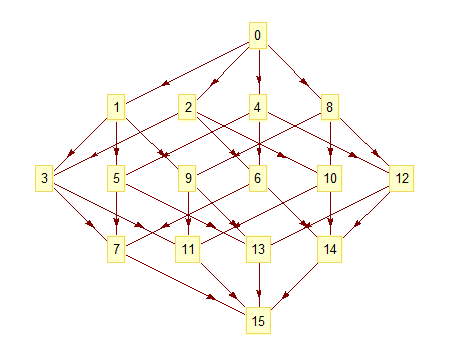
To understand our design, one must first realize that we apply a partial order to the CA space. This means we can break rules into their primitives (see below image). The primitives, p0 and p1, are based on the central cell in the rule code. This new organization of the space produces interesting results. Now, the space looks like a lattice (see below). Each rule has neighbors that are only one bit apart from itself. We began to notice clusters of similar rules spread throughout the space. I developed a clustering algorithm and discovered "rule signatures". These signatures can define the behavior of an entire cluster of CA rules. For instance, the signature {{"S", "C", "C", "S"}, {"D", "D", "D", "C"}}, where p0 = {"S", "C", "C", "S"} and p1 = {"D", "D", "D", "C"}, will generate a Sierpinski triangle with a white background and black foreground in radius 1 a.k.a. the ECA space. All of the variations in our module use the same seed, which can be recomputed at any time. Currently, this example does not support more than 2 states and limits the radii to 1 & 2.
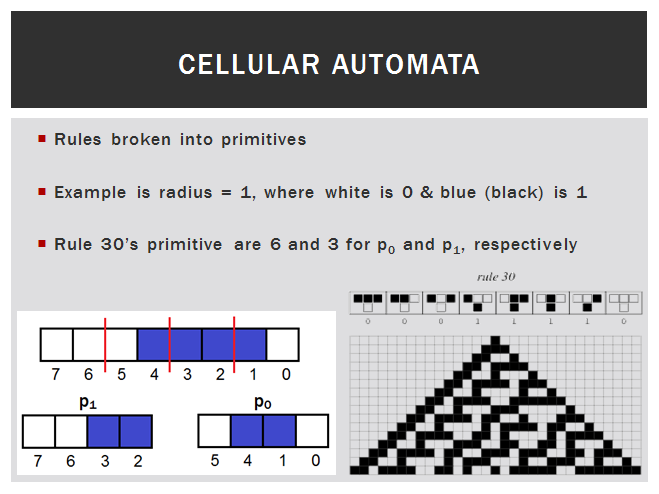
Cluster Signatures:
Cluster signatures are the power behind our probabilistic CA. To understand this, let's go back to the primitives. In p0, 0 is the base state, so any change to the primitive is denoted by a 1. The opposite is true for p1. In p1, the base state is one, so any change here is denoted by a 0. Translating this concept to our application, the signature that we used before was p0 = {"S", "C", "C", "S"} and p1 = {"D", "D", "D", "C"}. "C" denotes change so the bit in that position must flip from the base state. An "S" denotes that the position is static and must stay in the base state. "D" denotes that the position is dynamic; it can remain in the primitives' base state or flip and the output will not change. So the number of rules in a cluster is defined by the number of "D" positions in the signature. The cluster signature that we've been using contains 3 dynamic ("D") positions. So, there are 2^3 rules in that cluster. The "C" and "S" characters have a direct conversion to 0 and 1 according to the primitive in which they are located. Now we will have p0 = {0, 1, 1, 0} and p1 = {"D", "D", "D", 0}. From here, the positions marked "D" will be randomly chosen to form p0 = {0, 1, 1, 0} and p1 = {1, 0, 0, 0}. This rule evaluate to 1001 0010 = 146: a Sierpinski triangle in the ECA.
Tips and Tricks:
- All radius 1 rules can be mapped to radius 2 and vice versa. However, going from radius 2 to radius 1 will always lose information.
- Manually typing a rule into the "Base Rule" box will have no effect until checking the "Use Base Rule" box. The reason for this is to differentiate between using an exact rule from the box and using a probabilistic rule found by changing the cluster signature.
- If the radius is changed while the "Use Base Rule" box is checked, that specific rule will be mapped to the corresponding radius, not whatever signature is being used. If the "Use Base Rule" is not checked when the radius is changed, the current signature will be mapped to that radius.
- Complementing a rule while using one of the deterministic input settings may result in seemingly "blank" output. This is because the input will need to be "flipped" to the other deterministic setting.
- The limit of variations is set to 6 by default. Be aware that as the number of steps increase, the more computationally expensive it is to run each variation. In our tests, we found that the DynamicModule[] is given only so much resources. Once the threshold has been met, the evaluation will abort. To fix this, just lower either the variation count or the number of evaluation steps.
Cluster Signatures to Try:
- Triangles with tendrils: p0 = CCCS, p1 = SDDD, Input: DETERMINISTIC
- Rips from top in triangles: p0 = CDDC, p1 = SCCC, Input: DETERMINISTIC
- Rips on a veil: p0 = CDDD, p1 = SDDC, Input: STOCHASTIC
- Seashell patterns: p0 = DSSC, p1 = SCCC, Input: STOCHASTIC
- Other seashell patterns: p0 = SCCS, p1 = DDDC, Input: STOCHASTIC
- Roots or lightning: p0 = DDDD, p1 = SDDD, Input: STOCHASTIC
Please feel free to add-on to what we've done. Post ideas, solutions, and comments to further this investigation into probabilistic cellular automata.
 Attachments:
Attachments: