Here is another approach. The equation for an ellipse centered at (xc, yc, zc} with semimajor axes {a, b, c} and oriented with respect to the data coordinate system by Euler angles {[Alpha], [Beta], [Gamma]} is described by matrix methods. Given the equation LHS ==1, the sum of (LHS-1)^2 over the data is used as an error function. FindMinimum is used to determine the values of the parameters which minimize the error. This determines not only the semimajor axes, but also the center and orientation of the best-fit ellipsoid.

(* Equation for an ellipse centered at (xc,yc,zc} with semimajor axes \
{a,b,c} and oriented with respect to the data coordinate system by \
Euler angles {\[Alpha],\[Beta],\[Gamma]} is described by matrix \
methods *)

(* rotation of semimajor axes *)
rot = EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}];

(* the transpose *)
rotT = Transpose@rot;

(* diagonalized form *)
amat = DiagonalMatrix[{1/a^2, 1/b^2, 1/c^2}];

(* coordinate vectors *)
cmat = {{x - xc}, {y - yc}, {z - zc}};

(* the transpose *)
cmatT = Transpose@cmat;

(* this forms the left hand side of LHS \[Equal]1 *)
lhs = Simplify[cmatT.rotT.amat.rot.cmat][[1, 1]];
In[10]:= (* the square error from LHS \[Equal]1 for a single {x,y,z} \
point and given parameter set *)
squareError[{x_, y_, z_}, xc_, yc_, zc_, a_, b_, 
   c_, \[Alpha]_, \[Beta]_, \[Gamma]_] = (lhs - 1)^2;

(* find the parameter set which minimizes the error sum over the data \
*)
{residual, fit} = FindMinimum[
  {
   Plus @@ (squareError[#, xc, yc, zc, a, b, 
        c, \[Alpha], \[Beta], \[Gamma]] &) /@ data1,
   0 <= \[Alpha] < Pi, 0 <= \[Beta] < Pi, 0 <= \[Gamma] < Pi
   },
  {{xc, 2}, {yc, 0}, {zc, 0}, {a, 2}, {b, 2}, {c, 2}, {\[Alpha], 
    0}, {\[Beta], 0}, {\[Gamma], 0}}]

(* Out[11]= {0.044751062, {xc -> 2.0074857, yc -> 0.15231692, zc -> -0.10929044, a -> 4.311946, b -> 3.5987792, c -> 3.5830354, [Alpha] -> 0.00068328857, [Beta] -> 0.31168585, [Gamma] -> 0.85806301}} *)

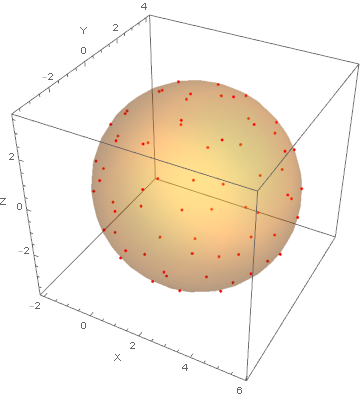
In[12]:= plot = 
 Show[ListPointPlot3D[data1, AxesLabel -> {"X", "Y", "Z"}, 
   PlotStyle -> Red, BoxRatios -> Automatic], 
  ContourPlot3D[
   Evaluate[1 == lhs /. fit], {x, -5, 6}, {y, -5, 5}, {z, -5, 5}, 
   ContourStyle -> Opacity[.3], Mesh -> None]]

Attachments:

I'm not sure what BoundedRegion does internally but it has a "FastEllipse" form specification. This is not a 'fit' as Daniel does (right?). i.e. with a fit you have data that is above/below the fit (or inside/outside) but this does not do that, it is always 'outside' of the data.

Depending what you are after this might be a alternative/better solution.

Yes, but those approaches are sometimes harder than need be (using nonlinear fitting where there is a formulation for a linear LS fit).

Hi I know this is not an efficient way to do it but I did this way. Note that data1=[{}]; is wrong notation, I changed to data1={{}};

 In[72]:= data3 = 
      Table[EuclideanDistance[data1[[j]], data1[[i]]], {i, 
        Length@data1}, {j, Length@data1}];
In[73]:= Max@data3

Out[73]= 8.50821

In[74]:= Position[data3, Max@data3]

Out[74]= {{5, 68}, {68, 5}}

In[75]:= data1[[5]]

Out[75]= {-1.47388, 2.66873, -0.915369}

In[76]:= data1[[68]]

Out[76]= {5.29808, -1.95733, 1.34955}



Show[HighlightMesh[ConvexHullMesh[data1], Style[2, Opacity[0.5]]], 
 Graphics3D[{Red, Line[{data1[[5]], data1[[68]]}]}], 
 Graphics3D[Point[data1]]]
Show[ListPointPlot3D[data1], 
 Graphics3D[{Red, Line[{data1[[5]], data1[[68]]}]}]]

Hi, It is hard for me to find it. What I can suggest is you need to split your data in two piece along the line (assume you have a plane that slice the ellipsoid in two half). Then find max the distance between two data. and similarly for other dimension..

BTW I modified @Marco Thiel ' s the code for this problem and here it is.

farpoints = 
  Take[data1[[#]] &@Flatten@Position[#, Max[#]] &@ DistanceMatrix[data1], 2];
distance = EuclideanDistance[First@farpoints , Last@farpoints ];
Show[ListPointPlot3D[{data1}], 
 Graphics3D[{{PointSize[Large], Red, 
    Point[#] & /@farpoints }, {Thick, Blue, Line[  farpoints ]}}], 
 ImageSize -> 500, 
 PlotLabel -> Framed@Style["distance = " <> ToString[distance], 20]]