Yes, the horizontal<-->vertical structures are to be expected.
The stadium is convex and in a zeroth approximation just a rectangle.
A rectangle shows the same horizontal<-->vertical structures:
dr = DiscretizeRegion[Rectangle[{-3/2, -1}, {3/2, 1}],
MaxCellMeasure -> 0.0005];
{vals, funs} = NDEigensystem[{-Laplacian[\[Psi][x, y], {x, y}],
DirichletCondition[\[Psi][x, y] == 0, True]}, \[Psi][x,
y], {x, y} \[Element] dr, 100,
Method -> {"Eigensystem" -> {"Arnoldi", "MaxIterations" -> 1000}}];
coords = MeshCoordinates[dr];
polys = Polygon[Developer`ToPackedArray[First /@ MeshCells[dr, 2]]];
frame[k\[Alpha]_] :=
Module[{ k = Floor[k\[Alpha]], f1, f2, \[Beta], max, vals2},
f1 = funs[[k]][[0]]; f2 = funs[[k + 1]][[0]];
\[Beta] = k\[Alpha] - k;
vals = Cos[Pi/2 \[Beta]]^2 (f1 @@@ coords) +
Sin[Pi/2 \[Beta]]^2 (f2 @@@ coords);
max = Max[Abs[vals]];
vals2 = vals/max;
Graphics[{EdgeForm[], Antialiasing -> True,
GraphicsComplex[coords, polys,
VertexColors -> (GrayLevel /@ (Abs[vals2]^0.5))],
Text[ If[Abs[k\[Alpha] - Round[k\[Alpha]]] <= 1/8,
Style[#, 18] &@ToString@Round[k\[Alpha]], ""], {0, -1.2}]},
PlotRange -> {{-1.6, 1.6}, {-1.3, 1.1}}]]
Manipulate[frame[k\[Alpha]], {k\[Alpha], 1, Length[funs] - 1}]
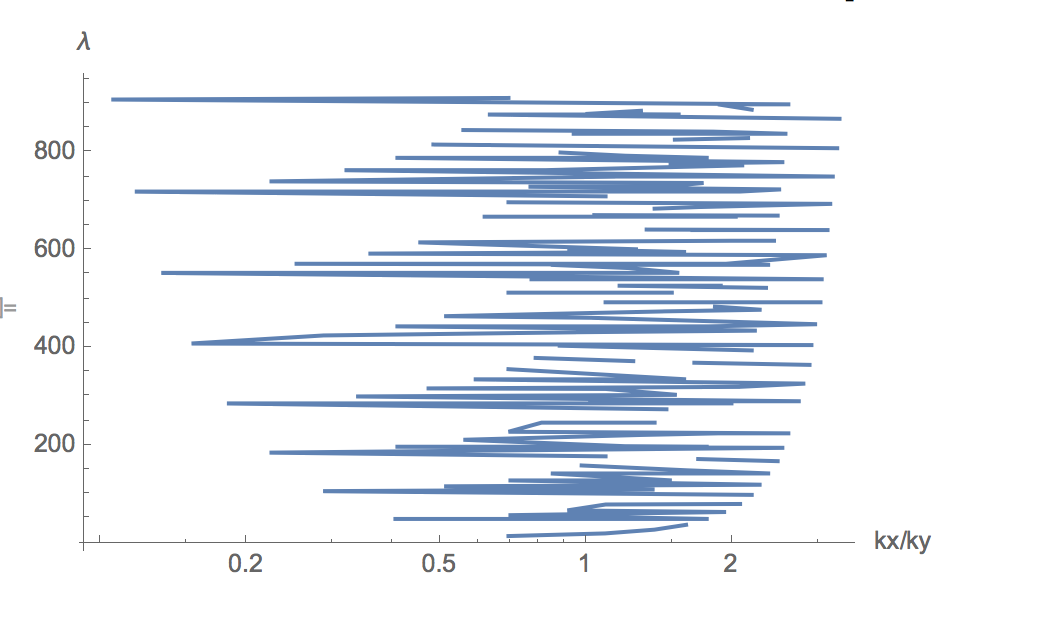
If ones takes the exact solution
-Laplacian[#, {x, y}]/# &@(Sin[kx x/3 Pi] Sin[ky y Pi]) // Simplify
1/9 (kx^2 + 9 ky^2) \[Pi]^2
and plots the ratio of the number of oscillations horizontally and vertically as the ratio kx/ky,
one sees that periodically one gets horizontal and vertical structures
ListLogLinearPlot[Take[#, 200] &@ SortBy[Flatten[Table[
{Log[kx/ky], 1./9 (kx^2 + 9 ky^2) \[Pi]^2}, {kx, 100}, {ky,
100}], 1], Last[#] &], Joined -> True,
AxesLabel -> {"kx/ky", "\[Lambda]"}]
In a more complicated domains, e.g. a Christmas tree
https://www.youtube.com/watch?v=XL7xQMoouFE
the recurring structures can be of different types, e.g. certain
subdomains of the region.
