Group Abstract Group Abstract

Message Boards Message Boards

Avoid evaluation with HoldForm, ReleaseHold for InputField?

Erdem Uguz
Posted 9 years ago

Hello, I am working on creating a CDF file for a calculation where I do high-precision evaluation of functions such as N[func,40]. I wrote a Module that takes user function and rationalize it, this way I create a function with user input accuracy. (Shown Below). When I don't use an inputfield my module works well but with inputfield I can't prevent it to be evaluated.

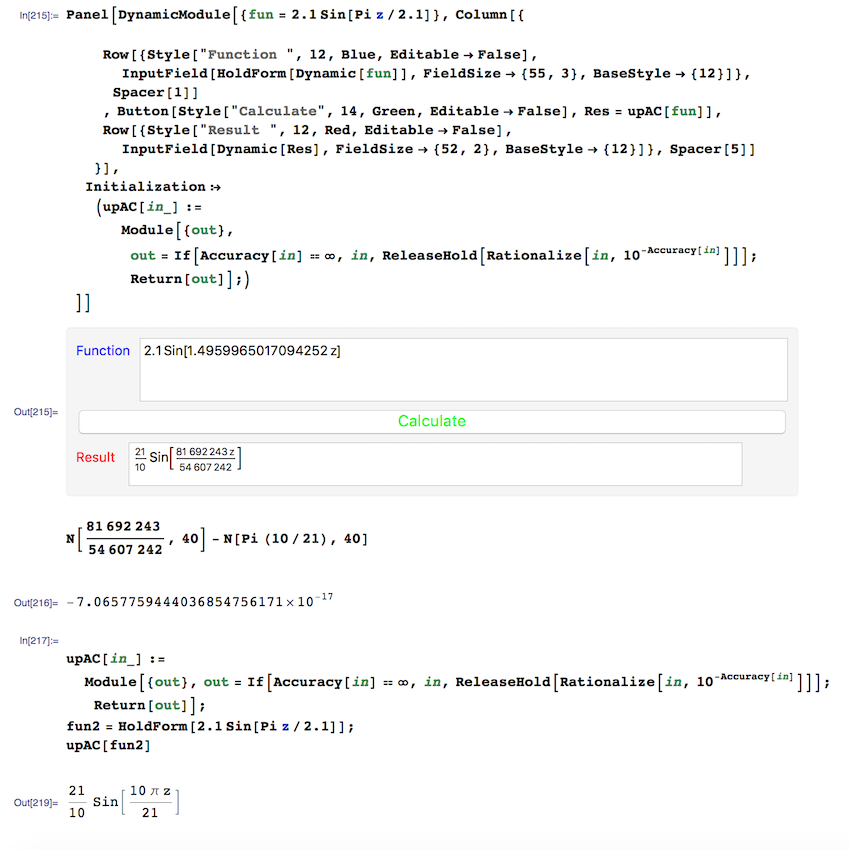
enter image description here

As you can see I need to avoid the evaluation so that I can evaluate the function in desired accuracy (number of digits). Any idea how I can do this?

Thank you

Erdem

Panel[DynamicModule[{fun = 2.1 Sin[Pi z/2.1]}, Column[{

    Row[{Style["Function ", 12, Blue, Editable -> False], 
      InputField[HoldForm[Dynamic[fun]], FieldSize -> {55, 3}, 
       BaseStyle -> {12}]}, Spacer[1]]
    , Button[Style["Calculate", 14, Green, Editable -> False], 
     Res = upAC[fun]],
    Row[{Style["Result ", 12, Red, Editable -> False], 
      InputField[Dynamic[Res], FieldSize -> {52, 2}, 
       BaseStyle -> {12}]}, Spacer[5]]
    }],
  Initialization :> (upAC[in_] := 
      Module[{out}, 
       out = If[Accuracy[in] == \[Infinity], in, 
         ReleaseHold[Rationalize[in, 10^-Accuracy[in]]]];
       Return[out]];)
  ]]

Also asked in http://mathematica.stackexchange.com/questions/133362/holdform-releasehold-for-inputfield
POSTED BY: Erdem Uguz
4 Replies
Sort By:
Erdem Uguz
Erdem Uguz
Posted 9 years ago

It is expected number of digits that is true but is it right? Forget about Sin. When I evaluate fg and fg2 with 40 digits fg2 has the right digits not fg . Because it is already evaluated before setting the accuracy after machine zero the digits are not right. My goal is to avoid that and evaluate fg when I need to evaluate with right digits. 

In[190]:= fg = Pi/2.1;
Print[fg];
fg2 = Pi/(21/10);
Print[fg2];
SetAccuracy[fg, 40]
SetAccuracy[fg2, 40]


During evaluation of In[190]:= 1.4959965017094252

During evaluation of In[190]:= (10 \[Pi])/21

Out[194]= 1.4959965017094252193174952481058426201344

Out[195]= 1.495996501709425351648877801561668040094
POSTED BY: Erdem Uguz
Hans Milton
Hans Milton
Posted 9 years ago

Hi,

Sorry, but I dont fully understand what you want to achieve.

However, if I declare Res as a Dynamic variable, outside of the DynamicModule itself, it returns the expected number of digits after pressing Calculate in the DynamicModule:

enter image description here
POSTED BY: Hans Milton
Hans Milton
Hans Milton
Posted 9 years ago

As an alternative to the answer you already received on stackexchange:

Panel[
  DynamicModule[{fun = HoldForm[2.1 Sin[Pi z/2.1]]},
    Column[{
      Row[{
        Style["Function ", 12, Blue, Editable -> False],
        InputField[Dynamic[fun], FieldSize -> {55, 3}, BaseStyle -> {12}]
      },
      Spacer[1]],
      Button[Style["Calculate", 14, Green, Editable -> False], Res = upAC[ReleaseHold@fun]],
      Row[{
        Style["Result ", 12, Red, Editable -> False],
        InputField[Dynamic[Res], FieldSize -> {52, 2}, BaseStyle -> {12}]
      },
      Spacer[5]]
    }],
    Initialization :>
      (
        upAC[in_] :=
        Module[
          {out},
          out = If[Accuracy[in] == \[Infinity], in, Rationalize[in, 10^-Accuracy[in]]];
          Return[out]
        ];
      )
  ]
]

enter image description here
POSTED BY: Hans Milton
Erdem Uguz
Erdem Uguz
Posted 9 years ago

Thank you but it is not working the way it should. Once you ReleaseHold it will go into the function after it is evaluated. 

In[5]:= N[81692243 /54607242, 40] - N[Pi/(21/10), 40]

Out[5]= -7.0657759444036854756171*10^-17

As you can see the result inside Sin can not anymore be evaluated with more than 16 Digits Accuracy.

POSTED BY: Erdem Uguz
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard