I could not find symbolic integral with erf function.
a = 1;
b = 2;
y = 3;
NIntegrate[Sqrt[x] Exp[-x/a] Exp[-(y - x)^2/b], {x, a, b}]
(*0.0867826*)
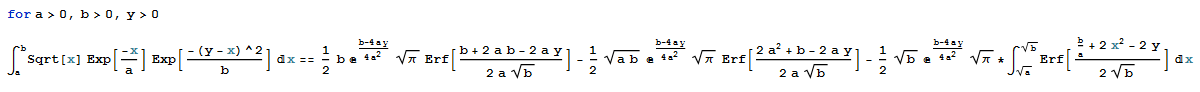
where:
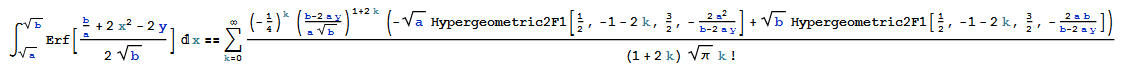
1/2 b E^((b - 4 a y)/(4 a^2)) Sqrt[\[Pi]] Erf[(b + 2 a b - 2 a y)/(2 a Sqrt[b])] -
1/2 Sqrt[a b] E^((b - 4 a y)/(4 a^2)) Sqrt[\[Pi]]Erf[(2 a^2 + b - 2 a y)/(2 a Sqrt[b])] -
1/2 Sqrt[b] E^((b - 4 a y)/(4 a^2)) Sqrt[\[Pi]]*NIntegrate[Erf[(b/a + 2 t^2 - 2 y)/(2 Sqrt[b])], {t, Sqrt[a], Sqrt[b]}]
(*0.0867826*)
Update:
Substituting x = t+y, t = a s-b/(2 a), s = m sqrt(b)/a and Integrating by parts:
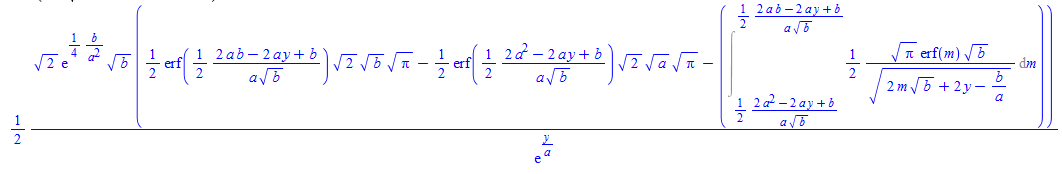
but the last integral MMA and Maple can't find.
If we simplify last integral to:
Integrate[Erf[m]/Sqrt[m + 1], m]
(* Integrate[Erf[m]/Sqrt[m + 1], m]*)
it is impossible to find antiderivative