Because is a general solution.
Solve[Cos[\[Phi]] == 1/Sqrt[2], \[Phi]]
(*{{\[Phi]-> ConditionalExpression[-(\[Pi]/4) + 2 \[Pi] C[1], C[1] \[Element] Integers]}, {\[Phi] -> ConditionalExpression[\[Pi]/4 + 2 \[Pi] C[1], C[1] \[Element] Integers]}}*)
C[1] [Element] Integers from ...-5,-4,-3,-2,-1,0,1,2,3,4,5...
Cos[#] & /@ Table[-(\[Pi]/4) + 2 \[Pi] n, {n, -5, 5, 1}]
(*{1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2],1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2]}*)
Cos[#] & /@ Table[\[Pi]/4 + 2 \[Pi] n, {n, -5, 5, 1}]
(*{1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2],1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2], 1/Sqrt[2]}*)
For interval (0,Pi)
Solve[{Cos[\[Phi]] == 1/ Sqrt[2] && 0 < \[Phi] < \[Pi]}, \[Phi]]
(*{{\[Phi] -> \[Pi]/4}}*)
For interval (-Pi,0)
Solve[{Cos[\[Phi]] == 1/ Sqrt[2] && -Pi < \[Phi] < 0}, \[Phi]]
(*{{\[Phi] ->- \[Pi]/4}}*)
.
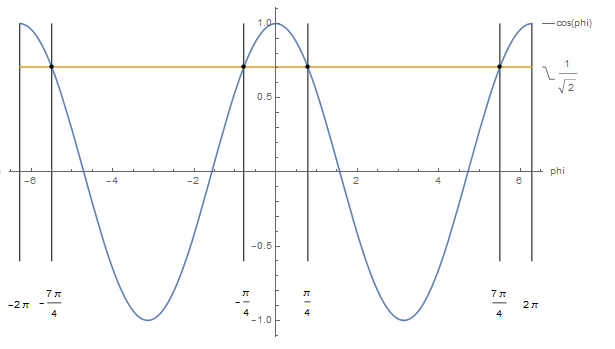
Plot[{Cos[phi], 1/Sqrt[2]}, {phi, -2 Pi, 2 Pi},
Epilog -> {PointSize[Medium],
Point[{{-(( 7 \[Pi])/4), 1/Sqrt[2]}, {-(\[Pi]/4), 1/
Sqrt[2]}, {\[Pi]/4, 1/Sqrt[2]}, {(7 \[Pi])/4, 1/Sqrt[2]}}]},
Prolog -> {Line[{{- 2 \[Pi], -0.6}, {- 2 \[Pi], 1}}],
Line[{{-(( 7 \[Pi])/4), -0.6}, {-(( 7 \[Pi])/4), 1}}],
Line[{{-( \[Pi]/4), -0.6}, {-( \[Pi]/4), 1}}],
Line[{{ \[Pi]/4, -0.6}, { \[Pi]/4, 1}}],
Line[{{(7 \[Pi])/4, -0.6}, {(7 \[Pi])/4, 1}}],
Line[{{ 2 \[Pi], -0.6}, { 2 \[Pi], 1}}],
Text[-(( 7 \[Pi])/4), {-(( 7 \[Pi])/4), -0.9}],
Text[- 2 \[Pi], {- 2 \[Pi], -0.9}],
Text[-( \[Pi]/4), {-( \[Pi]/4), -0.9}],
Text[ \[Pi]/4, { \[Pi]/4, -0.9}],
Text[( 7 \[Pi])/4, {( 7 \[Pi])/4, -0.9}],
Text[ 2 \[Pi], { 2 \[Pi], -0.9}]}, PlotLabels -> "Expressions",
AxesLabel -> {phi}]