I'm have found particular identity with Hypergeometric2F1.
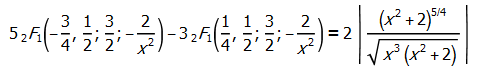
{Abs[(2 (2 + x^2)^(5/4))/Sqrt[x^3 (2 + x^2)]] ==
5 Hypergeometric2F1[-(3/4), 1/2, 3/2, -(2/x^2)] - 3 Hypergeometric2F1[1/4, 1/2, 3/2, -(2/x^2)]} /.
x -> {1/10, 1/5, 1.2, 1, 2, Pi} // N
(*True*)
Plot[{Abs[(2 (2 + x^2)^(5/4))/Sqrt[x^3 (2 + x^2)]], 5 Hypergeometric2F1[-(3/4), 1/2, 3/2, -(2/x^2)] -
3 Hypergeometric2F1[1/4, 1/2, 3/2, -(2/x^2)]}, {x, -1, 1}, PlotStyle -> {Red, {Green, Dashed}}, PlotRange -> {{-1, 1}, {0, 222}}]
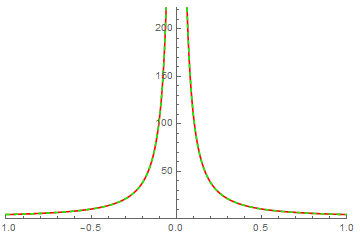
Are there many such identity's ? Maybe this has already been discovered?