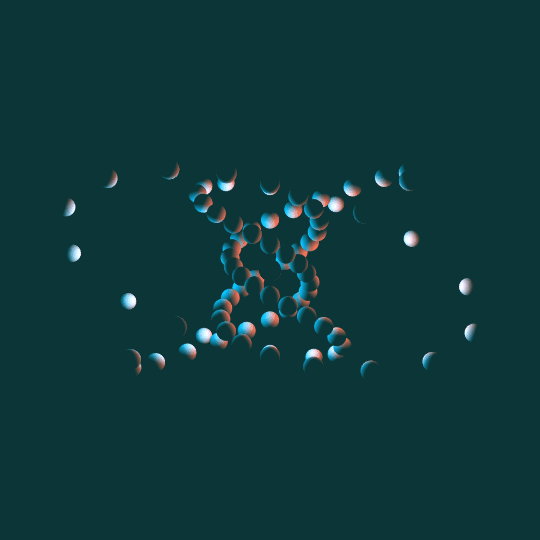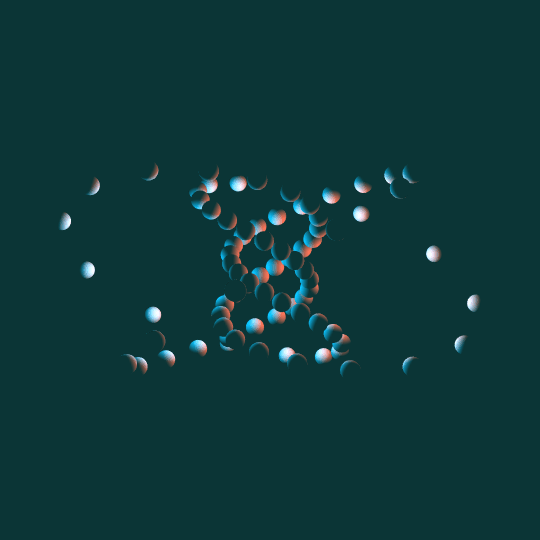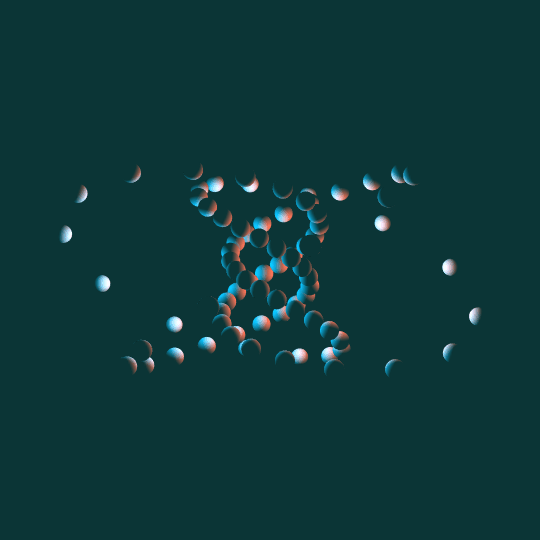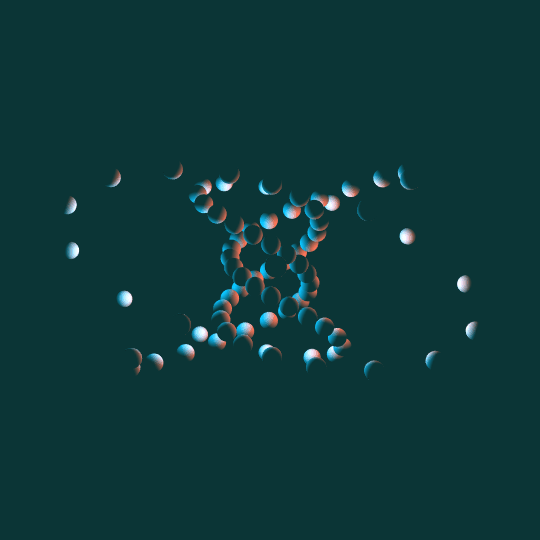
Come Around
Same basic idea as To Infinity and Inevitability: a bunch of little spheres following the path of a torus knot. This time the knot is a $(5,3)$-torus knot and the view is from the side rather than above. Other than that and the different lighting, the underlying math is basically identical.
One note: as with almost everything I do involving tori, I'm using the Clifford torus as my underlying ideal torus, and then stereographically projecting to 3-dimensional space.
Here's the code:
Stereo3D[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)};
pqtorus[t_,ϕ_, p_, q_] := 1/Sqrt[2] {E^(p I (t + ϕ/p)), E^(q I t)};
With[{viewpoint = {0, 3, 0}, n = 80,
cols = RGBColor /@ {"#f54123", "#0098d8", "#0b3536"}},
Manipulate[
Graphics3D[{Sphere[#, .1] & /@
Table[Stereo3D[Flatten[ReIm /@ pqtorus[t + ϕ, 0, 5, -3]]], {t, 0, 2 Pi, 2 Pi/n}]},
PlotRange -> 2.7,
ViewPoint -> viewpoint, ViewAngle -> Pi/9,
ViewVertical -> {0, 0, -1}, Boxed -> False,
Background -> cols[[-1]],
Lighting -> {{"Point", cols[[1]], {3/4, 0, 0}},
{"Point", cols[[2]], {-3/4, 0, 0}}, {"Ambient", cols[[-1]], viewpoint}},
ImageSize -> 540],
{ϕ, 0, 2 Pi/n}]
]