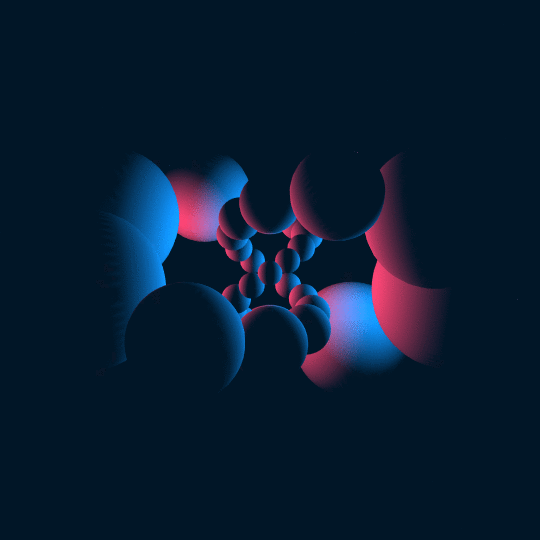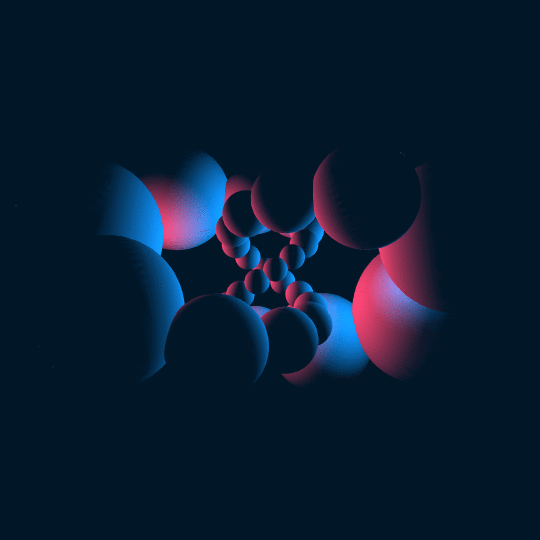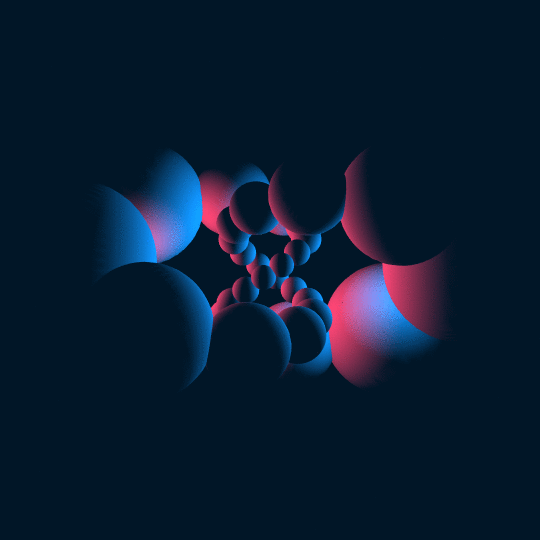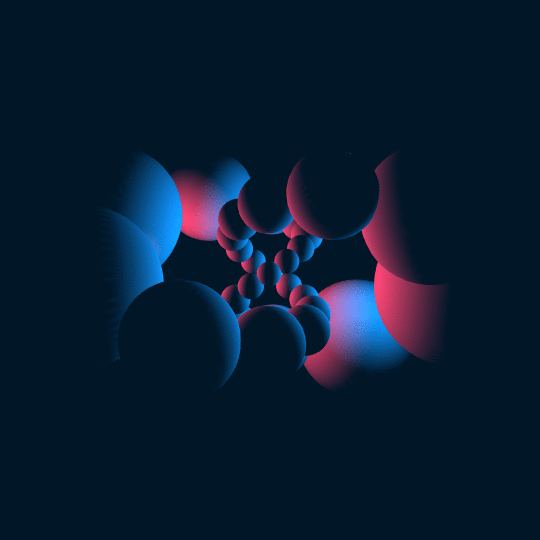
Intertwine

This a similar concept to Stereo Vision in that I start with a torus knot in the 3-sphere and stereographically project it to 3-space. In this case, the knot is just a trefoil knot. In Stereo Vision I took a tube of uniform thickness around a $(24,23)$ torus knot and projected it down; in this case, I put spheres of radius $0.3$ around 30 uniformly-spaced points along the knot and projected those down. In the animation the points just traverse along the knot. The stereographic image of a sphere is a sphere, so the result is a bunch of spheres in space, but they no longer have uniform radius or spacing.

That's all conceptually pretty straightforward. The tricky bit is that the spheres downstairs are not centered on the stereographic images of the corresponding points up in the 3-sphere. I could have used Sphere, but that would have required me to figure out what points they're centered on and what their radii are, which I was too lazy to do. Instead, I used spherical coordinates to parametrize the spheres upstairs and then just composed the parametrization with stereographic projection and used ParametricPlot3D.

This is what's going on with the sphere function in the code: given a point p on the 3-sphere, the orthogonal complement in $\mathbb{R}^4$ is a 3-dimensional linear subspace whose intersection with the 3-sphere is a great 2-sphere. Given an orthonormal basis $\{b_1, b_2, b_3\}$ for the linear subspace, we get spherical coordinates $q(\theta,\phi) = (\cos \theta \sin \phi) b_1 + (\sin \theta \sin \phi) b_2 + (\cos \phi) b_3$ on the sphere. Then any other lesser sphere at constant distance $d$ from $p$ can be parametrized by $\theta$ and $\phi$ by just taking $(\cos d) p + (\sin d) q(\theta,\phi)$. This is the same strategy as used in Interference, Tetra, and Spin Around, just one dimension up.

As for the code, first we need to define stereographic projection and the parametrization of the knot:

Stereo3D[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)};

pqtorus[t_, ?_, p_, q_] := 1/Sqrt[2] Flatten[ReIm /@ {E^(p I (t + ?/p)), E^(q I t)}];

The code below is for a Manipulate which is slightly lower quality than the final animation. Because spherical coordinates become singular at the poles, just doing ParametricPlot3D without any options produces little black splotches at the poles. I fixed this in the final version using MaxRecursion -> 5, but that's a little too slow for an interactive version.

DynamicModule[{p = 3, q = 2, n = 15, 
  viewpoint = 10. {Cos[-4 ?/5], Sin[-4 ?/5], 0}, point, basis,
   sphere, cols = RGBColor /@ {"#FF304F", "#118DF0", "#011627"}},
 point[t_, ?_] := pqtorus[t + ?, 0, p, q];
 basis[t_, ?_] := Orthogonalize[NullSpace[{point[t, ?]}]];
 sphere[t_, ?_, ?_, ?_] := 
  Cos[.3] point[t, ?] + Sin[.3] Total[{Cos[?] Sin[?], Sin[?] Sin[?], Cos[?]}*basis[t, ?]];
 Manipulate[
  ParametricPlot3D[
   Evaluate[Table[Stereo3D[sphere[t, ?, ?, ?]], {t, 0., 2 ? - 2 ?/(q n), 2 ?/(q n)}]],
   {?, 0, ?}, {?, 0, 2 ?},
   Mesh -> None, PlotRange -> 4, ViewPoint -> viewpoint, 
   ViewAngle -> ?/32, ImageSize -> 540, Boxed -> False, 
   PlotStyle -> White, ViewVertical -> {0, 0, 1}, Axes -> None, 
   Background -> cols[[-1]], 
   Lighting -> {{"Point", cols[[1]], 2 {Cos[7 ?/10], Sin[7 ?/10], 0}}, 
      {"Point", cols[[2]], 2 {Cos[17 ?/10], Sin[17 ?/10], 0}} , 
      {"Ambient", cols[[-1]], viewpoint}}
   ],
  {?, 0., 2 ?/(q n)}]
 ]