I have tried to do it in two different ways.
1.
Using ParametricRegion:
R = ParametricRegion[{Xt[X2, Th3, La1, La2, La3, La4,
La5] /. {X2 -> X2in,
La3 -> La3in} /. {Th3 -> Th3in,
La4 -> La4in, La5 -> La5in}, Yt[X2, Th3, La1, La2, La3, La4, La5] /. {X2 -> X2in,
La3 -> La3in} /. {Th3 -> Th3in,
La4 -> La4in, La5 -> La5in}}, {{La1, dA1min, dA1max}, {La2,
dA2min, dA2max}}];
And trying to represent it by:
Region[R]
This is not able to give a result (it is still running after about 10h and 8GB of RAM).
2.
Using ParametricPlot
ParametricPlot[{{Xt[X2, Th3, La1, La2, La3, La4, La5],
Yt[X2, Th3, La1, La2, La3, La4, La5]}} /. {X2 ->
X2min, Th3 -> Th3min, La3 -> dA3min, La4 -> dA4min, La5 -> dA5min}, {La1, dA1min, dA1max}, {La2, dA2min, dA2max}, AspectRatio
-> Automatic]
This is able to give a result relatively fast (40s and <2GB of RAM).
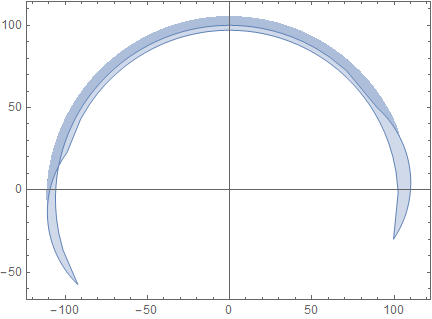
But unfortunately, ParametricPlot can't plot regions depending on more than 2 variables.
Just to give some insight into the problem, (Xt, Yt) give the position of a point from a body in a machine. I need to obtain the 'range of action' of this point. I need to find the contour of the area (or the area itself) in which the point can be located. The problem is that the point depends on 5 (6) variables.