Power Surge

Continuing in the spirit of Map, In Balance, and Correlations, another Mercator projection of phenomena on the sphere.

In this case, the underlying object is the tetrahedron, or more precisely its vertices:

tetverts = Prepend[Permutations[{-1/Sqrt[3], -1/Sqrt[3], 1/Sqrt[3]}], {1/Sqrt[3], 1/Sqrt[3], 1/Sqrt[3]}]

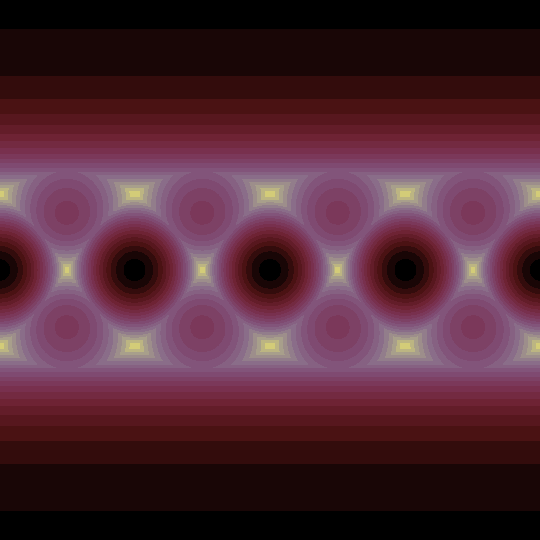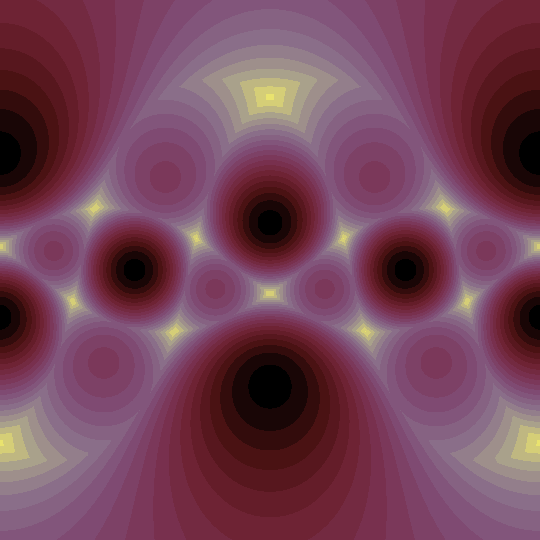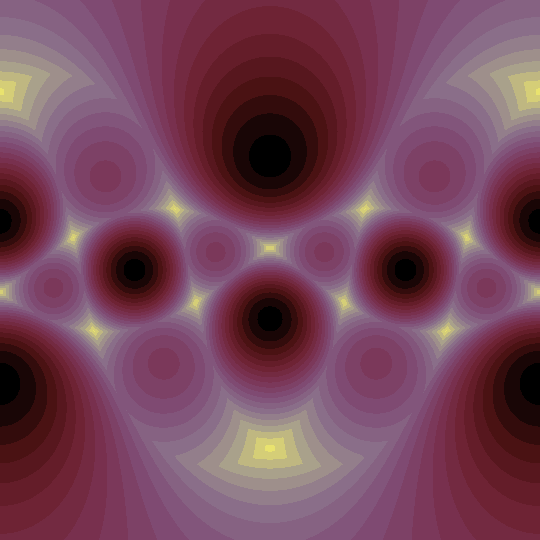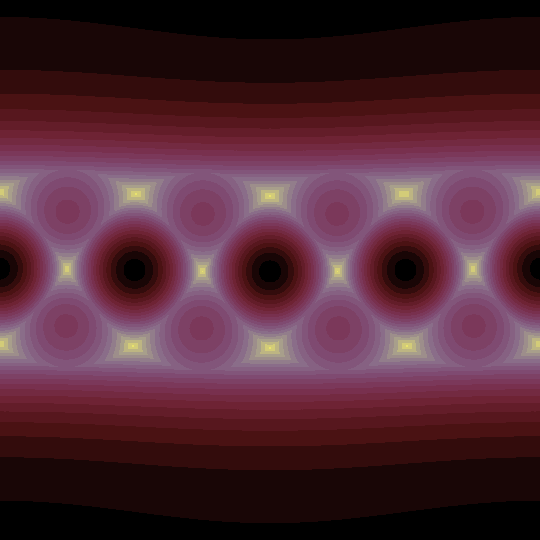
Now, the animation shows the Mercator projection of the level sets of the function which takes the sum of the absolute values of the dot products with the four vertices of the tetrahedron as they rotate around the $x$-axis:

InverseMercator[{x_, y_}] := {Sech[y] Cos[x], Sech[y] Sin[x], Tanh[y]};
TetTotalDotProduct[{x_, y_}, ?_] = FullSimplify[
   Total[Abs /@ (InverseMercator[{x, y}].RotationTransform[?, {1, 0, 0}][#] & /@ tetverts)],
   -? < x < ? && -? < y < ? && 0 < ? < ?/2];

Finally, then, I just choose a color scheme and try to make it look nice:

Manipulate[
 ContourPlot[
  TetTotalDotProduct[{x, y}, ?],
  {x, -?/2, 3 ?/2}, {y, -?, ?},
  Frame -> False, ImageSize -> 540, ContourStyle -> None, PlotRangePadding -> -0.01,
  Contours -> Range[2 Sqrt[2/3.] + (2 - Sqrt[2])/(20 Sqrt[3]), 4/Sqrt[3], (2 - Sqrt[2])/(10 Sqrt[3])],
  ColorFunction -> (ColorData["PlumColors"][1 - #] &)],
 {?, 0, ?/2}]

Note that the global maximum of $4/\sqrt{3}\approx 2.31$ is achieved at the midpoints of the edges (the 6 black points; recall that the Mercator projection is really a map to the cylinder, so the left and right edges are identified). There are also 8 local maxima (in purple) at the vertices of the tetrahedron and their antipodes (or, if you like, the vertices of the dual tetrahedron), where the sum of the dot products is exactly $2$. The global minimum value of $2\sqrt{2}/\sqrt{3}\approx 1.63$ is achieved at the 12 points which lie on the lines passing through the three points on each face with barycentric coordinates $1/2 : 1/4 : 1/4$, $1/4 : 1/2 : 1/4$, or $1/4 : 1/4 : 1/2$ (yellow points).

The function is non-differentiable along the great circles perpendicular to the vertices of the tetrahedron (as you would expect, since each such great circle is the locus of non-differentiability for one of the absolute-value-of-dot-product-with-a-vertex functions), which appear as the ghostly curves in the animation.