Many of you have seen the strandbeest (from Dutch, meaning beach-beast). These PVC tube animals created by Theo Jansen walk along the beach and are wind powered:

Years ago (2009 to be more exact) I made a post on my blog about the movement of the legs, as evidenced by the still-nicely-working Mathematica notebook:
At the time the proportions of the legs were not known publicly so I meticulously studied frames of (low quality) YouTube videos. I made the following diagram in Illustrator of what I thought I saw:
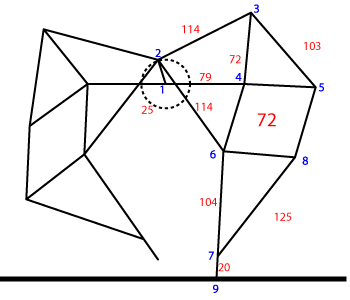
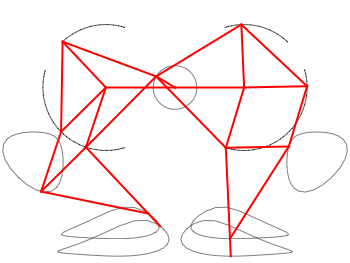
On the left the length of the legs in red, and in blue the numbers of the joints. On the right the trajectory of the joints that I calculated at the time in Mathematica. It's funny that my blog does not exist any more (for years actually), but these images live on, as I found out when I looked for strandbeest on Google Images:
My images! But not on my website! Nice to see people still use it. Now, in 2016, I saw these files on my laptop, and thought: is there finally more known about them? Well yes, there is! The exact proportions are now known and there is tons and tons of videos, lectures, 3D-printable strandbeest models, interviews with Theo Jansen and other stuff! So now we can find the exact dimensions readily on the internet:

Notice that I (wrongly) assumed that the legs had 'feet'! oops! I was very happy to see that my lengths were not that wrong though! Let's recreate the strandbeest. We do so by first creating a function that quickly finds the intersection of two circles:
Clear[FindPoint, FindLines]
FindPoint[p1 : {x1_, y1_}, p2 : {x2_, y2_}, R_, r_, side_] := Module[{d, x, y, vc1, vc2, p, sol, sol1, sol2, s1, s2, sr},
d = N@Sqrt[(x2 - x1)^2 + (y2 - y1)^2];
x = (d^2 - r^2 + R^2)/(2 d);
y = Sqrt[R^2 - x^2];
vc1 = Normalize[{x2 - x1, y2 - y1}];
vc2 = Cross[vc1];
p = {x1, y1} + x vc1;
{sol1, sol2} = {p + y vc2, p - y vc2};
s1 = Sign[Last[Cross[Append[(p2 - p1), 0], Append[(sol1 - p1), 0]]]];
s2 = Sign[Last[Cross[Append[(p2 - p1), 0], Append[(sol2 - p1), 0]]]];
sr = If[side === Left, 1, -1];
Switch[sr, s1,
sol1
,
s2
,
sol2
]
]
This finds on the side 'side' (Left/Right) the intersection point of two circles positioned at p1 and p2, with radii R and r, respectively. And now we can easily compute all the little vertices/joints of our beast:
FindLines[\[Theta]_] := Module[{p1, p2, p3, p4, p5, p6, p7, p8, p10, p11, p12, p13, p14, p15},
{p1, p2, p3, p4, p5, p6, p7, p8, p10, p11, p12, p13, p14, p15} = FindPoints[\[Theta]];
{{p1, p2}, {p2, p3}, {p3, p4}, {p1, p4}, {p2, p6}, {p4, p6}, {p3, p5}, {p4, p5}, {p5, p8}, {p6, p8}, {p6, p7}, {p7, p8}, {p1,
p11}, {p10, p11}, {p2, p10}, {p2, p13}, {p11, p13}, {p10, p12}, {p11, p12}, {p12, p14}, {p13, p14}, {p13, p15}, {p14, p15}}
]
FindPoints[\[Theta]_] := Module[{p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12, p13, p14, p15, p16},
p1 = {0, 0};
p4 = {38, -7.8};
p11 = {-38, -7.8};
p2 = 15 {Cos[\[Theta]], Sin[\[Theta]]};
p3 = FindPoint[p2, p4, 50, 41.5, Left];
p6 = FindPoint[p2, p4, 61.9, 39.3, Right];
p5 = FindPoint[p3, p4, 55.8, 41.5, Left];
p8 = FindPoint[p5, p6, 39.4, 36.7, Left];
p7 = FindPoint[p6, p8, 49, 65.7, Right];
p10 = FindPoint[p2, p11, 50, 41.5, Right];
p13 = FindPoint[p2, p11, 61.9, 39.3, Left];
p12 = FindPoint[p10, p11, 55.8, 41.5, Right];
p14 = FindPoint[p12, p13, 39.4, 36.7, Right];
p15 = FindPoint[p13, p14, 49, 65.7, Left];
{p1, p2, p3, p4, p5, p6, p7, p8, p10, p11, p12, p13, p14, p15}
]
Now we can plot it easily:
trajectoriesdata = (FindPoints /@ Subdivide[0, 2 Pi, 100])\[Transpose];
Manipulate[
Graphics[{Arrowheads[Large], Arrow /@ trajectoriesdata, Thick, Red, Line[FindLines[\[Theta]]]},
PlotRange -> {{-150, 150}, {-120, 70}},
ImageSize -> 800
]
,
{\[Theta], 0, 2 \[Pi]}
]
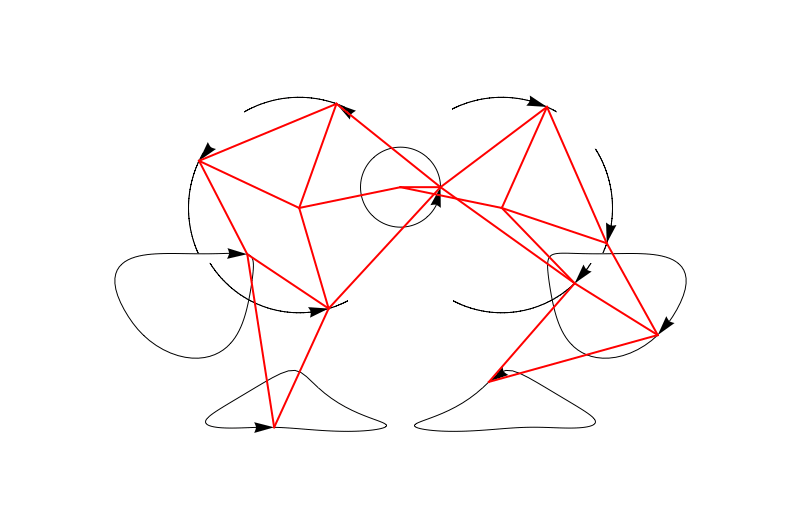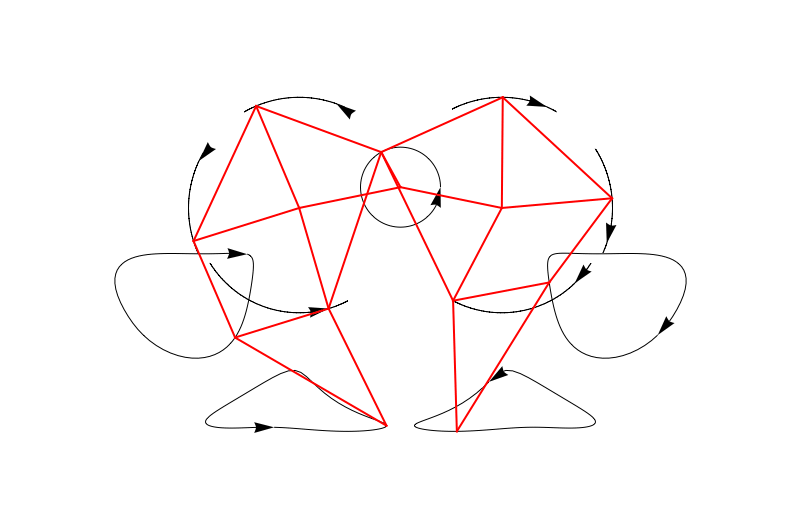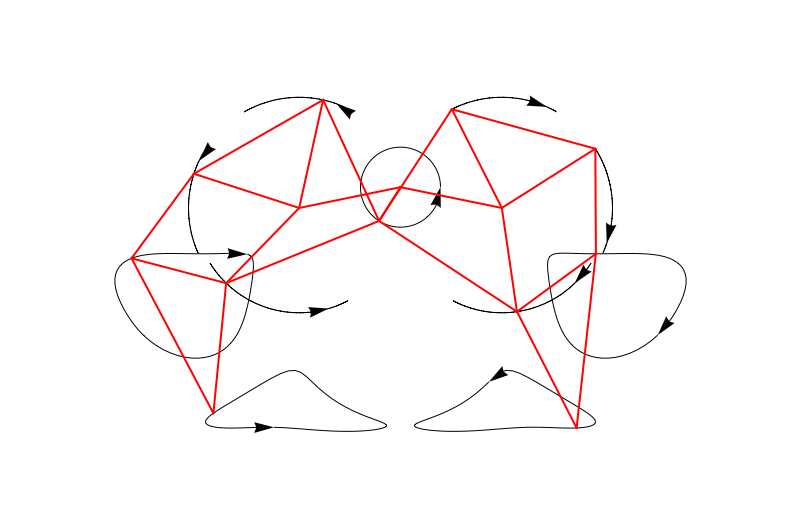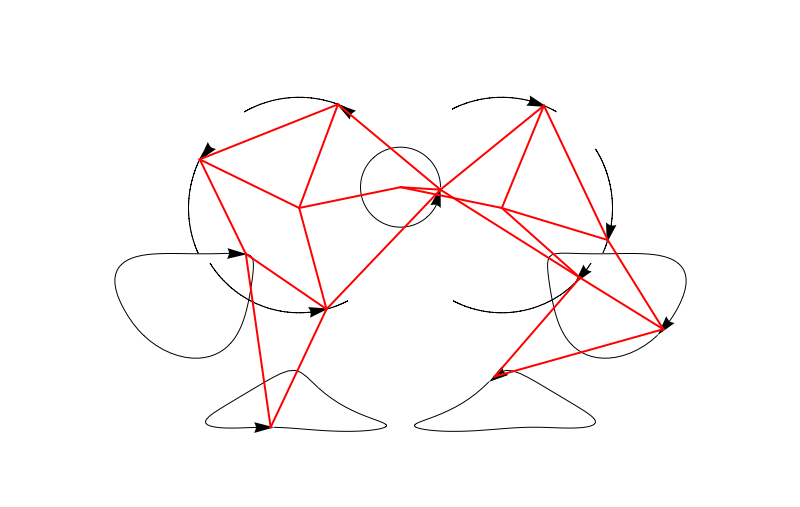
We can also make an entire bunch of legs at the same time and make a 3D beast!
Manipulate[
mp = 60;
n = 12;
\[CurlyPhi] = Table[Mod[5 \[Iota], n, 1], {\[Iota], 1, n}];
Graphics3D[{Darker@Yellow, Table[
Line[
Map[Prepend[mp \[Iota]],
FindLines[\[Theta] + \[CurlyPhi][[\[Iota]]] (2 Pi/n)], {2}]],
{\[Iota], n}
]
, Black, Line[{{mp 1, 0, 0}, {mp n, 0, 0}}]
}
,
Lighting -> "Neutral",
PlotRangePadding -> Scaled[.1],
PlotRange -> {{-mp, (n + 1) mp}, {-150, 150}, {-150, 150}},
Boxed -> False,
ImageSize -> 700
]
,
{\[Theta], 0, 2 \[Pi]}
]

From the side we can look at how the legs of 4-pair-legged and 6-pair-legged versions of the beasts work:
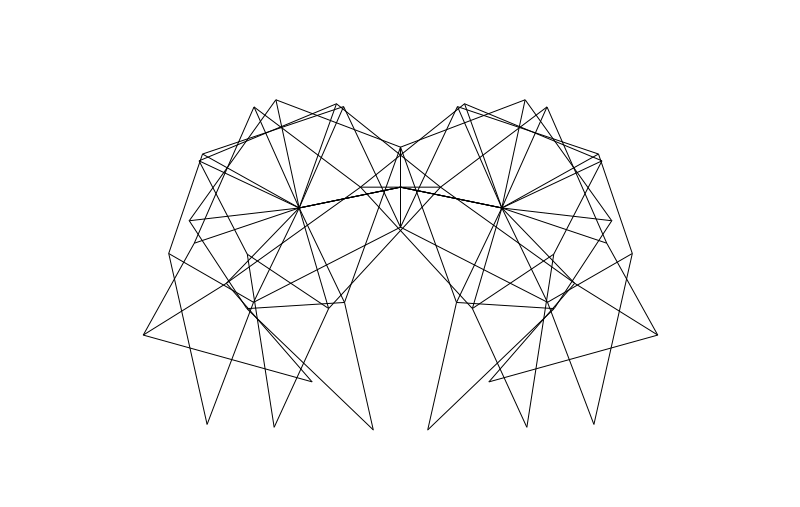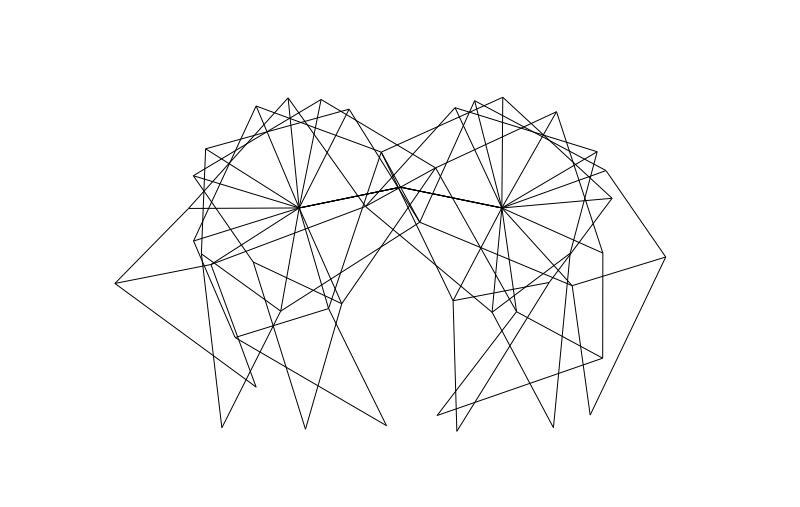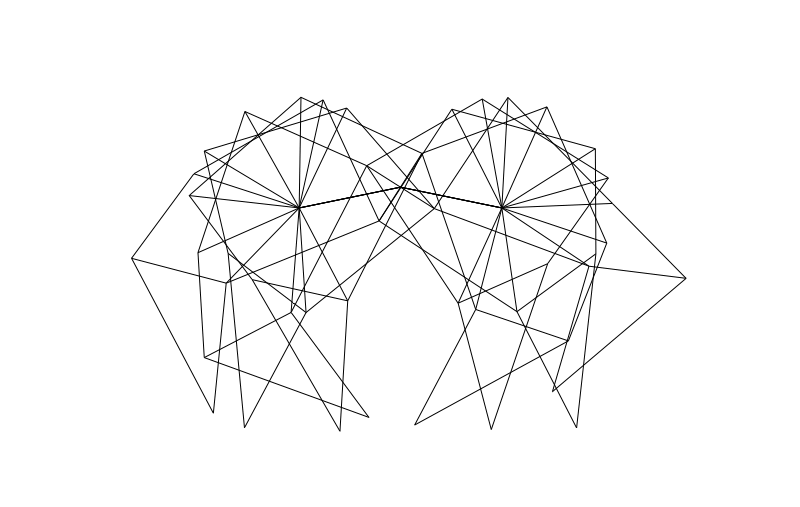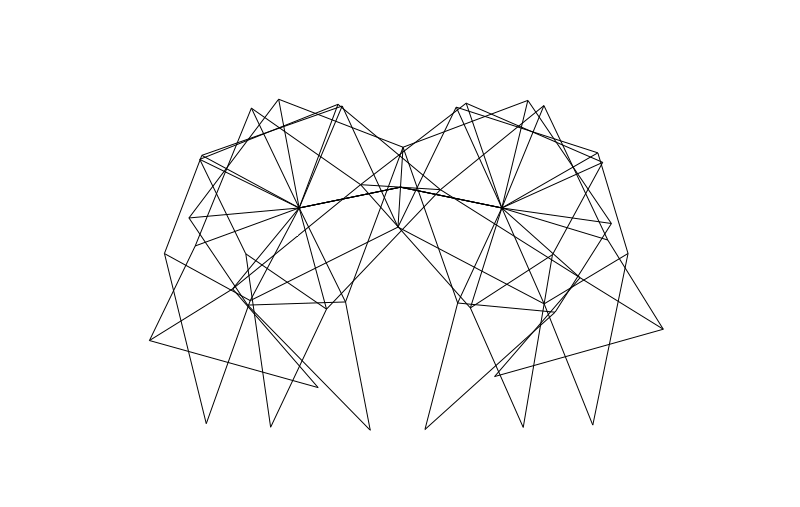
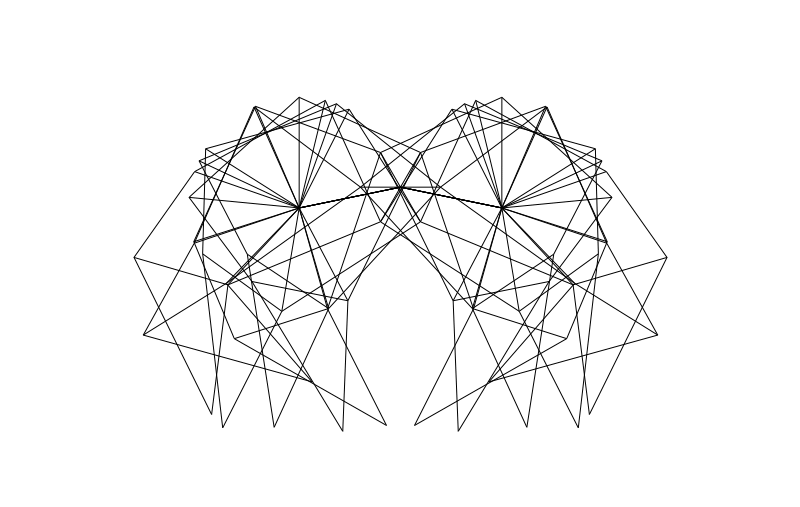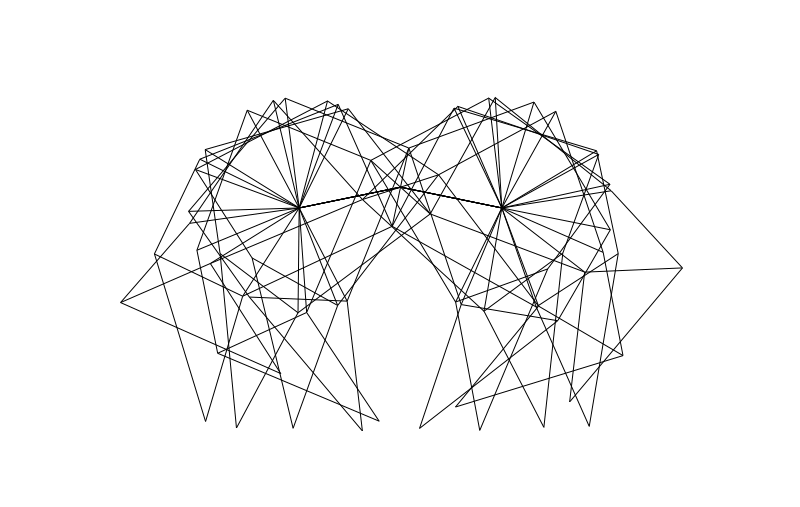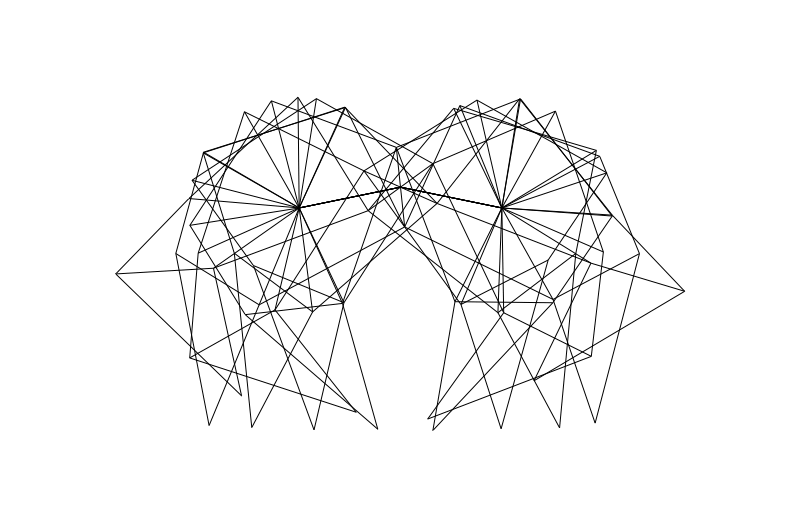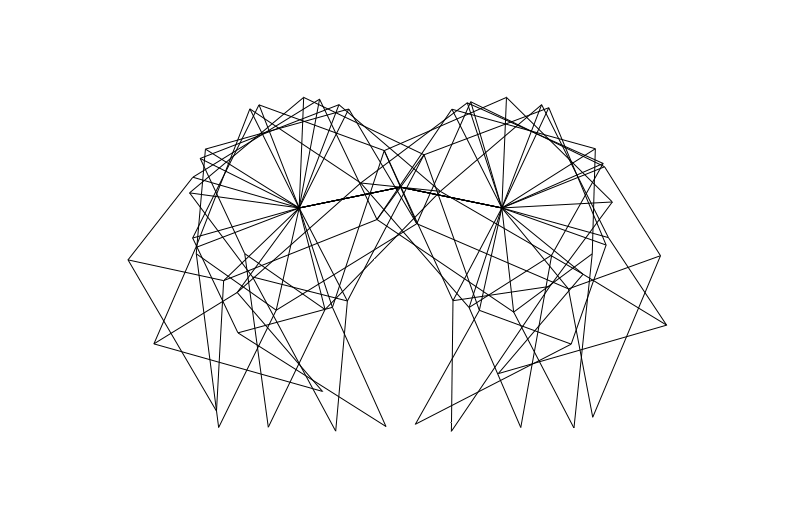
Hope you enjoyed this! Perhaps someone else can make this thing actually walk over a (bumpy) surface?