User Portlet

I am a high school student at Columbia Prep in New York City. I have been programming in Mathematica since December 2014 and it is one of my favorite activities. During the summer of 2015, I participated in the Mathematica Summer Camp in which I furthered my knowledge of Mathematica. I have been in the Wolfram Mentorship Program in which I work on projects under the guidance of my mentor, Todd Rowland, since September 2015 and am still in it. I have done research into the problem of equally spacing n points on a sphere and I am currently developing videos to teach Mathematica to students in a fun way. I also now am very interested in Machine Learning and have made a question classifier with Mathematica that is very accurate. I also am currently doing research at the NYU Data Science Center with Professor Dennis Shasha into Machine Learning and Computational Biology.

My Demonstrations:

• Lattice Squares of Integer Area
• Tiling a Hexagon
• 3D Snowflake Fractals
• Folding Nets into Polyhedra

Here is my 3D Snowflake Fractals Demonstration:

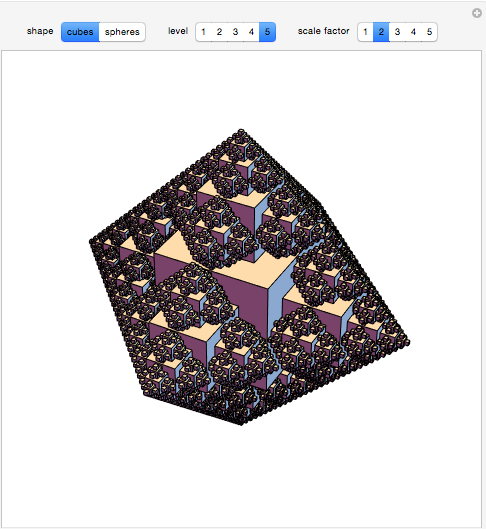
Manipulate[
 Graphics3D[{
   If[shape == "cubes",
    box = Cuboid[{0, 0, 0}],
    box = Scale[Sphere[{0, 0, 0}], 1/2]
    ];
   flake =
    {box, 
     Translate[Scale[box, scaleFactor], {scaleFactor/2 + .5, 0, 0}], 
     Translate[box, {scaleFactor/2 + .5, scaleFactor/2 + .5, 0}], 
     Translate[box, {scaleFactor/2 + .5, 0, scaleFactor/2 + .5}], 
     Translate[box, {2*(scaleFactor/2 + .5), 0, 0}], 
     Translate[box, {scaleFactor/2 + .5, -(scaleFactor/2 + .5), 0}], 
     Translate[box, {scaleFactor/2 + .5, 0, -(scaleFactor/2 + .5)}]};
   Table[
    flake = {flake,
      Translate[
       flake, {(scaleFactor/2 + .5)*
         scaleFactor^x, (scaleFactor/2 + .5)*scaleFactor^x, 0}], 
      Translate[
       flake, {(scaleFactor/2 + .5)*scaleFactor^x, 
        0, (scaleFactor/2 + .5)*scaleFactor^x}], 
      Translate[flake, {2*(scaleFactor/2 + .5)*scaleFactor^x, 0, 0}], 
      Translate[
       flake, {(scaleFactor/2 + .5)*
         scaleFactor^x, -1*(scaleFactor/2 + .5)*scaleFactor^x, 0}], 
      Translate[
       flake, {(scaleFactor/2 + .5)*scaleFactor^x, 
        0, -1*(scaleFactor/2 + .5)*scaleFactor^x}],

      If[shape == "cubes", 
       Cuboid[{Total[scaleFactor^# &@Range[0, x, 1]]
         , 1/2 - scaleFactor^(x + 1)/2, 1/2 - scaleFactor^(x + 1)/2},
        {Total[scaleFactor^# &@Range[0, x, 1]] + scaleFactor^(x + 1), 
         1/2 - scaleFactor^(x + 1)/2 + scaleFactor^(x + 1), 
         1/2 - scaleFactor^(x + 1)/2 + scaleFactor^(x + 1)}],
       Sphere[{Total[scaleFactor^# & /@ Range[0, x]] + 
          scaleFactor^(x + 1)/2 - 1/2, 0, 0}, scaleFactor^(x + 1)/2]
       ]
      },
    {x, 1, level - 1}
    ];
   If[shape == "cubes",
    flake, Translate[flake, {1/2, 1/2, 1/2}]]
   }, ImageSize -> 450, Axes -> False, Boxed -> False, 
  ViewAngle -> 20 Degree, SphericalRegion -> True],
 Row[{
   Spacer[20],
   Control@{shape, {"cubes", "spheres"}},
   Spacer[20],
   Control@{{level, 3}, 1, 5, 1, ControlType -> Setter},
   Spacer[20],
   Control@{{scaleFactor, 2, "scale factor"}, 1, 5, 1, 
     ControlType -> Setter}
   }],
 TrackedSymbols :> {shape, level, scaleFactor}, 
 ContinuousAction -> False
 ]