Dear Colleagues,
I am currently studying, in particular, the HypergeometricU function (
confluent hypergeometric function) for a statistics problem.
(using Mathematica 9.0.1.0)
Unfortunately, Mathematica seems to be able to calculate the function only with gaps, in the regions where I would like to evaluate it.
See for example:
LogPlot[HypergeometricU[10.5, 31, x], {x, 0, 300}]
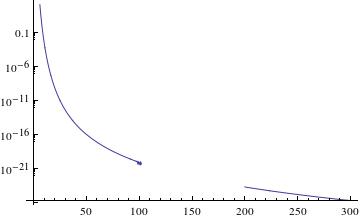
Is there a way of calculating the function values within such gaps?