If you are using V8, then you would have to change the syntax a little bit as follows:
R = 1 + 10^-15;
eqns = (2 (1 - (r/R)^2)) D[rho[r, z],z] == (r D[rho[r, z], r, r] + D[rho[r, z], r])/r;
bcs = {rho[R, z] == 0, Derivative[1, 0][rho][10^-19, z] == 0,rho[r, 0] == 1};
sol = Quiet@NDSolve[{eqns, bcs}, rho, {r, 10^-19, R}, {z, 0, 10},Method -> {"MethodOfLines",
"DifferentiateBoundaryConditions" -> {True,"ScaleFactor" -> 10^4}}] ;
If you want to plot the solution from {-R, R}, then you can just mirror the solution.
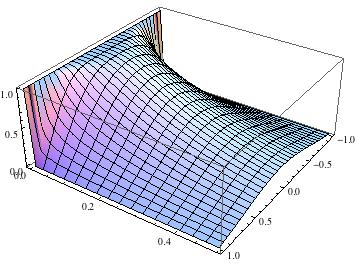
Show[Plot3D[Evaluate[rho[r, z] /. sol], {r, 0, R}, {z, 0, 0.5},PlotRange -> All] ,
Plot3D[Evaluate[rho[-r, z] /. sol], {r, -R, 0}, {z, 0, 0.5}]]