Hi Tahar,

Function $Erf$ lends itself well to series analysis, as the function is asymptotically flat, so eventually a truncated series will work well enough for approximation.

The Series and InverseSeries functions are very fast when operating on a particular function:

Series[Exp[-x^2], {x, 0, 20}]
Sqrt[Pi]/2 Series[Erf[x], {x, 0, 20}]
InverseSeries[%, y]

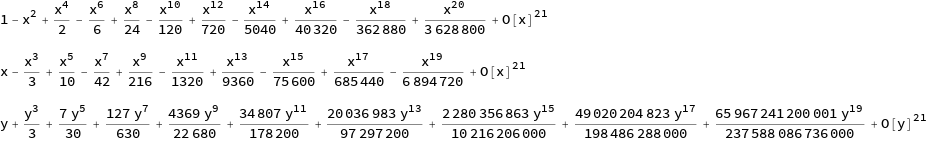
You can also look convergence using parametric plot,

Row[Show[
    Plot[Sqrt[Pi]/2 Erf[x], {x, -10, 10}, PlotStyle -> Blue],
    MapThread[
     ParametricPlot[Evaluate[{Normal@InverseSeries[
           Sqrt[Pi]/2 Series[Erf[x], {x, 0, #1}], y], y}],
       {y, -2, 2}, PlotStyle -> #2] &,
     {10 Range[5], Blend[{Red, Orange}, #/5] & /@ Range[5]}],
    PlotRange -> {{-#, #}, {-1.5, 1.5}}, ImageSize -> 400
    ] & /@ {2, 10}]

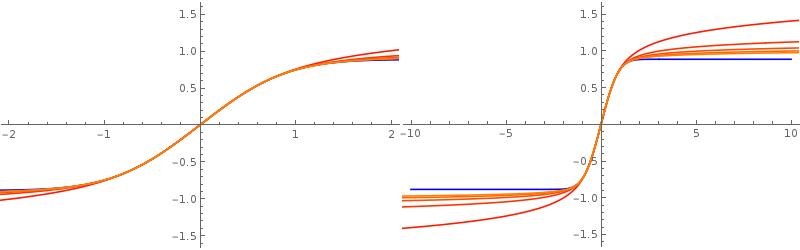
Up to $\pm 2$, convergence looks pretty good , but the divergence can be seen over a wider domain.

Mathematica is good at automating all of this, but you might also wonder: how does InverseSeries calculate the expansion coefficients? In one sense, this an easy to answer question because the inversion problem can be solved with arbitrary value expansion coefficients (Cf. fast, symbolic DIY inversion algorithms here). Any algorithm simply involves arithmetical transformation of the input series expansion coefficients. Example calculations for your function of choice are available at: Error Function Series Inversion ( work in progress ).

Brute-force, ennumerative methods can produce a number of expansion coefficients, but usually do not produce the best closed-form results. Fortunately, in practice, closed-form results are not always necessary for applications.

Another option is to use something like InverseErf. Before you do so, it's useful to at least check and see if the expansion coefficients are as expected.

Series[InverseErf[2/Sqrt[Pi] x], {x, 0, 10}]

Should match the wiki example calculation above, or the OEIS reference is A092676 / A132467 .