Where is the geographic center of the US? According to the National Geologic Survey, the center of the conterminous US is at 39°50'N 98°35'W, and the center of all US states (including Alaska and Hawaii) is at 44°58'N 103°46'W. The thing is, the center of a region on the globe is not entirely well defined. That is, there are multiple ways of characterizing the center of a region like the US.

With Projections

Well how did the NGS do it? The NGS published their results for the center of the conterminous US in 1918. They took a map of the US, cut out a piece of cardboard in the shape of that map, and then found its center of mass by hanging it from various points. The center of mass of this piece of cardboard, they said, was analogous to the center of the conterminous US.

What they essentially measured is the centroid of the US in some projection. The key point is "in some projection". With another projection you could get a different result. The NGS didn't try many projections, but they did consider this problem. However, as Oscar S. Adams somewhat hilariously says in a paper presenting some of the NGS's methods,

[...] almost any one of the methods already outlined will give a point that is accurate enough for all practical purposes. As a matter of fact, it is hardly conceivable that such a point should meet any 'practical purpose' in any case.

In 1918, checking this claim, that the projections will not make too big a difference, would have required a lot of cardboard and a lot of time, but now it is much easier to investigate this.

First, let's get a 2D MeshRegion for the US. To get a 2D region, we have to use some projection, so we will use the equirectangular projection where the x-coordinate is the longitude and the y -coordinate is the latitude. This makes it easy to convert this to a geo-Polygon by just wrapping GeoPosition around each vertex, and also makes it easier to put this in all sorts of projections.

We need to get a geo-Polygon for the conterminous US and convert it into a MeshRegion. To do this, we can just call DiscretizeGraphics.

r = DiscretizeGraphics[Polygon/@Map[Reverse, Entity["Country", "UnitedStates"]["Polygon"][[1,1]],{2}]]

RegionUnion[
    DiscretizeGraphics@Map[Polygon]@Map[Reverse, Entity["Country", "UnitedStates"]["Polygon"][[1,1]],{2}],
    DiscretizeGraphics@Map[Polygon]@Map[Reverse, Entity["AdministrativeDivision", {"Hawaii", "UnitedStates"}]["Polygon"][[1,1]],{2}],
    DiscretizeGraphics@Map[Polygon]@Map[Reverse, Entity["AdministrativeDivision", {"Alaska", "UnitedStates"}]["Polygon"][[1,1]],{2}]
]

Everything we do with the conterminous US will also apply to all of the states, and in fact to any other region on the planet. We'll start by defining a function that projects a MeshRegion like r into whatever map projection we want.

projectMesh[r_, proj_] := MeshRegion[GeoGridPosition[GeoPosition[Reverse/@MeshCoordinates[r]], proj][[1]], MeshCells[r,2]]

projectMesh[r, "Robinson"]

Now we can easily create a function that finds the centroid of this region, and then uses GeoGridPosition to take that centroid from the projection's coordinates to a GeoPosition.

meshCentroid[r_, proj_] := GeoPosition@GeoGridPosition[RegionCentroid[projectMesh[r, proj]], proj]

In[]:= meshCentroid[r, "Mercator"]

Out[]= GeoPosition[{40.1393, -99.3083}]

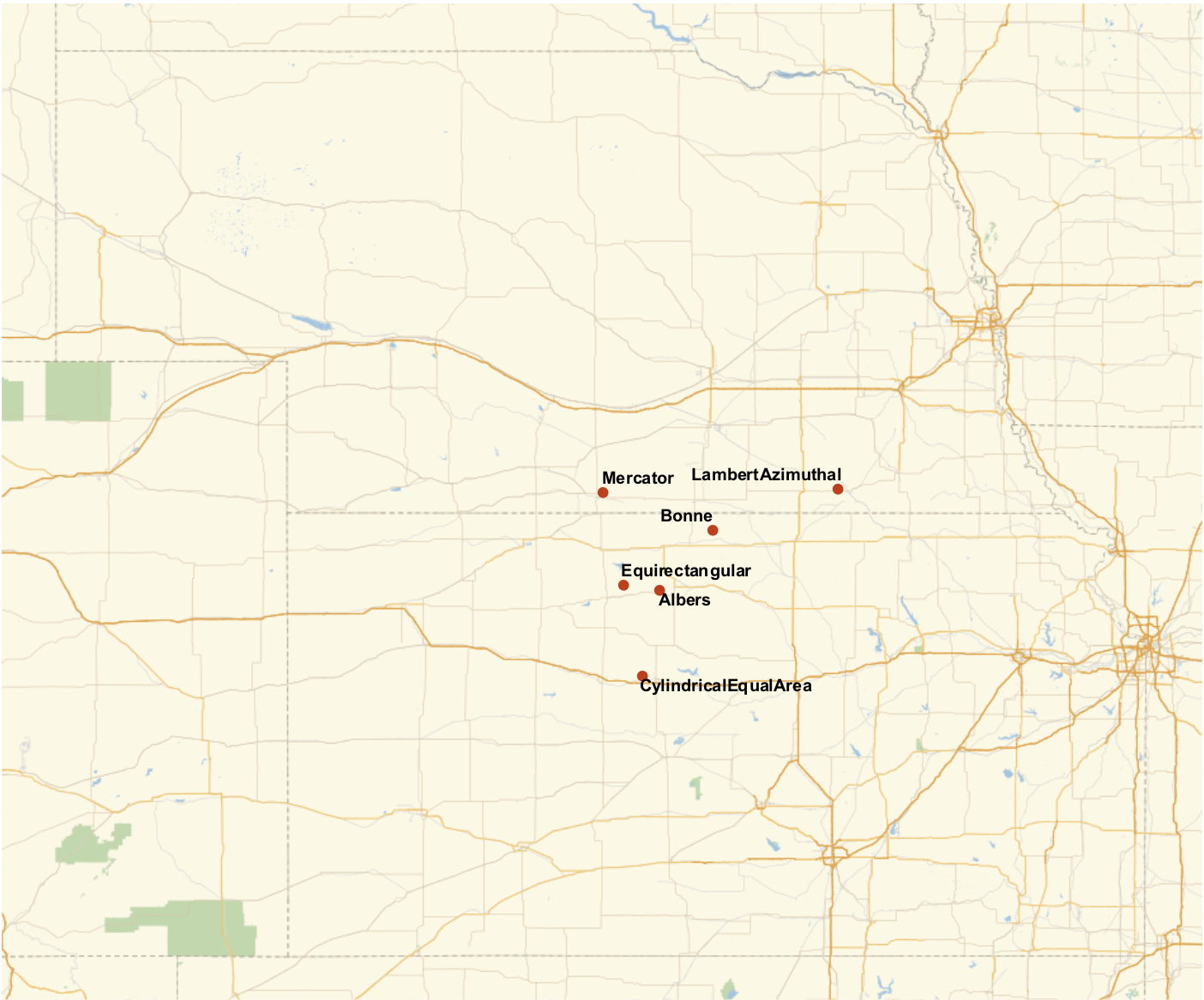
Now, we can try this with a few projections and put them on a map.

GeoListPlot[
    Labeled[meshCentroid[r,#],#]&/@{"Equirectangular","Mercator","Albers","CylindricalEqualArea","Bonne","LambertAzimuthal"},
    GeoRange->"AdministrativeDivision", ImageSize->700]

Let's do try this with lots of projections! This gets us all of the commonly named projections that can project the conterminous US.

 projs =
    Quiet@Select[
        Complement[
        GeoProjectionData[],
        GeoProjectionData["UTMZone"],
        GeoProjectionData["SPCS27"],
        GeoProjectionData["SPCS83"]],
    MeshRegionQ@projectMesh[r,{#,"Centering"->{0,0}}]&]

Out[]= {"Airy", "Aitoff", "Albers", "AmericanPolyconic", "ApianI", \
"ApianII", "ArdenClose", "Armadillo", "AugustEpicycloidal", \
"AzimuthalEquidistant", "BaconGlobular", "Balthasart", \
"BehrmannEqualArea", "BipolarObliqueConicConformal", \
"BoggsEumorphic", "Bonne", "Bottomley", "BraunConicStereographic", \
"BraunCylindrical", "BraunII", "BSAMCylindrical", "Cassini", \
"Collignon", "ConicEquidistant", "ConicPerspective", \
"ConicSatelliteTracking", "Craster", "CrasterCylindricalEqualArea", \
"CylindricalEqualArea", "CylindricalEquidistant", \
"CylindricalSatelliteTracking", "DenoyerSemielliptical", \
"EckertGreifendorff", "EckertI", "EckertII", "EckertIII", "EckertIV", \
"EckertV", "EckertVI", "EquatorialStereographic", "Equirectangular", \
"Euler", "FoucautEqualArea", "FoucautStereographic", \
"FournierGlobularI", "FournierII", "GallIsographic", \
"GallStereographic", "GinzburgI", "GinzburgII", "GinzburgIV", \
"GinzburgIX", "GinzburgPseudoCylindrical", "GinzburgV", "GinzburgVI",
  "GoodeHomolosine", "GottElliptical", "GottMugnoloElliptical", \
"Hammer", "Hatano", "HerschelConicConformal", "HoboDyer", \
"Hyperelliptical", "KarchenkoShabanova", "KavrayskiyV", \
"KavrayskiyVII", "Lagrange", "LambertAzimuthal", \
"LambertConformalConic", "LambertConformalConicNGS", \
"LambertConicEqualArea", "LambertCylindrical", "Larrivee", \
"Loximuthal", "Maurer", "McBrydeThomasFlatPolarParabolic", \
"McBrydeThomasFlatPolarQuartic", "McBrydeThomasFlatPolarSinusoidal", \
"McBrydeThomasI", "McBrydeThomasII", "Mercator", "MillerCylindrical", \
"MillerCylindricalII", "MillerPerspective", "Mollweide", "MurdochI", \
"MurdochII", "MurdochIII", "NaturalEarth", "Nell", "NellHammer", \
"ObliqueMercator", "OrteliusOval", "PavlovCylindrical", \
"PeirceQuincuncial", "PutninsP1", "PutninsP1Prime", "PutninsP2", \
"PutninsP3", "PutninsP3Prime", "PutninsP4Prime", "PutninsP5", \
"PutninsP5Prime", "PutninsP6", "PutninsP6Prime", "QuarticAuthalic", \
"RectangularPolyconic", "Robinson", "Shield", "SinuMollweide", \
"Sinusoidal", "SnyderMinimumError", "SpaceObliqueMercator", \
"Stereographic", "Times", "TissotConicEqualArea", "ToblerI", \
"ToblerII", "TransverseMercator", "TrapezoidalMercator", \
"TrystanEdwards", "UPSNorth", "UPSSouth", "UrmayevCylindricalII", \
"UrmayevCylindricalIII", "UrmayevI", "UrmayevPseudoCylindrical", \
"VanDerGrinten", "VanDerGrintenII", "VanDerGrintenIII", \
"VanDerGrintenIV", "WagnerI", "WagnerII", "WagnerIII", "WagnerIV", \
"WagnerIX", "WagnerV", "WagnerVI", "WagnerVII", "WagnerVIII", \
"WerenskioldI", "Werner", "Wiechel", "WinkelI", "WinkelII", \
"WinkelSnyder", "WinkelTripel"}

Now many of these projections actually have a few parameters. Of particular importance here is a parameter called "Centering". The thing is, we don't want WL to try to be clever in picking some center for the projection if that center isn't going to be consistent. For now, we can just set the "Centering" for each projection to GeoPosition[{0,0}].

GeoListPlot[Labeled[meshCentroid[r, {#,"Centering"->{0,0}}],#]&/@projs, GeoRange->"AdministrativeDivision", ImageSize->1000]

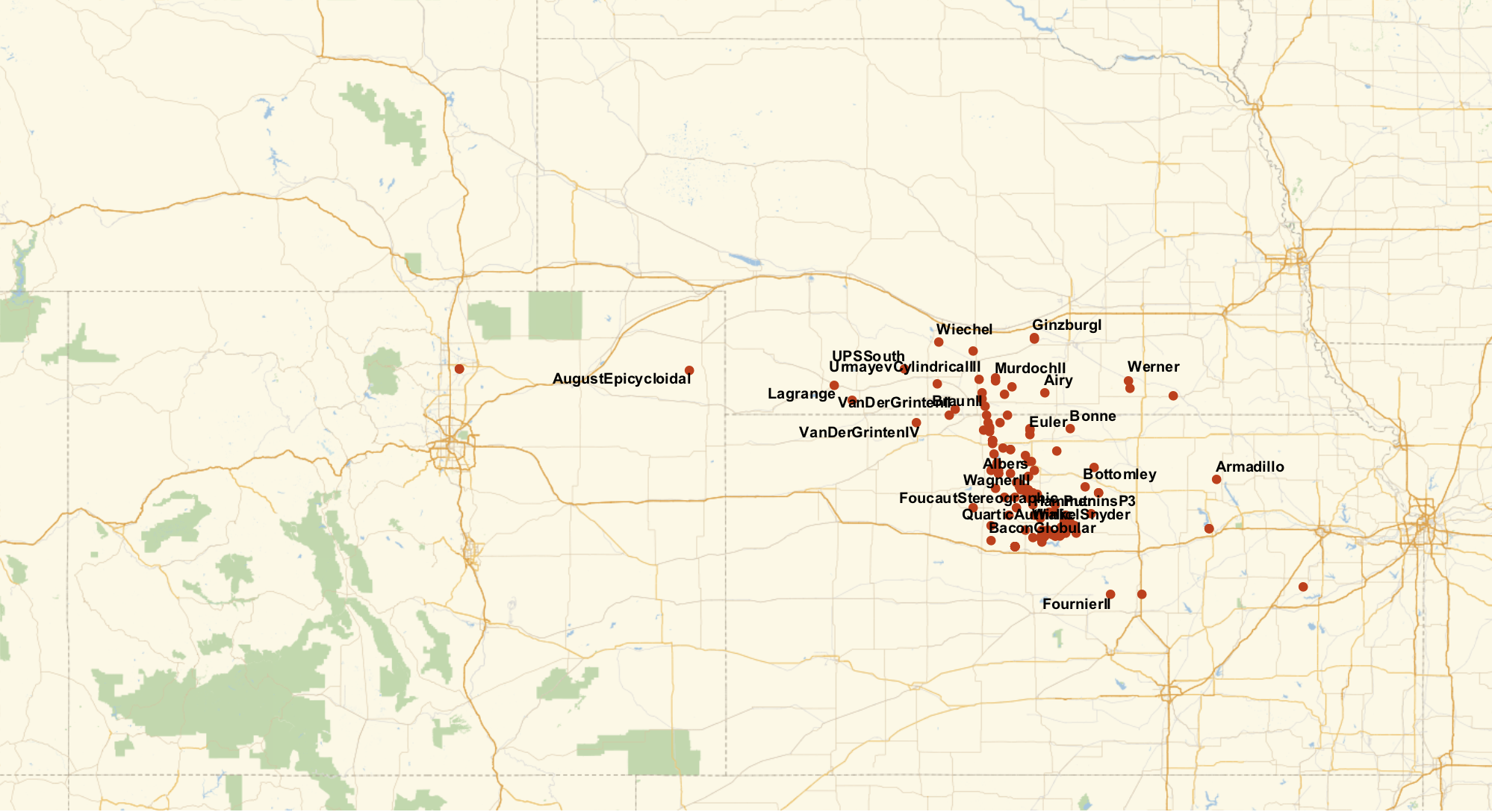
So it looks like we have a bit of a spread. Most of the projections give the center of the US in Kansas, with a few in Nebraska, and just a couple of oddballs in Colorado.

That "Centering" parameter is causing some silly things though. For some projections, "Centering"->GeoPosition[{0,0}] is fine. But for others, we get things like this.

projectMesh[r, {"LambertAzimuthal", "Centering"->GeoPosition[{0,0}]}]

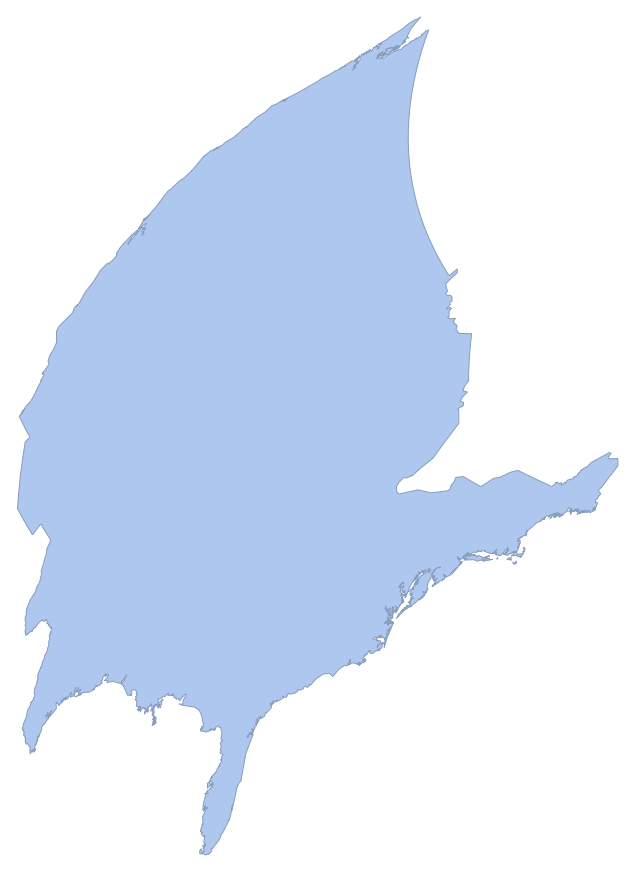
What we really want is to center the projection on the center of the US, but of course we don't know the center of the US (or at least there is no unique center). There are a few ways we could try to get around this. I like the following method. We start with "Centering"->GeoPosition[{0,0}] and find the center of the US with meshCentroid. Then we run it again, this time with "Centering" set to the output of that. Basically, we run this recursively where we set the "Centering" to the last output again and again until it stabilizes. This can be expressed nicely with NestWhile or NestWhileList.

geoPositionFilter[g:GeoPosition[{__?NumberQ}]] := g
geoPositionFilter[_] := Missing[]

centroidPaths =
    AssociationMap[Function[proj,
        NestWhileList[
            Quiet@Check[geoPositionFilter@meshCentroid[r,{proj,"Centering"->#}],Missing[]]&,GeoPosition[{0,0}],
            !MissingQ[#2]&&GeoDistance[#1,#2]>0.1mi&,
            2,
            10
        ]],
        projs];

centroids = centroidPaths[[All, -1]];

We can take a look at the series of projections we get while it stabilizes for some projection.

projectMesh[r, {"LambertAzimuthal","Centering"->#}]&/@centroidPaths["LambertAzimuthal"]

And we can look at the series of centers as it stabilizes.

GeoListPlot[centroidPaths["LambertAzimuthal"], Joined -> True, ImageSize -> 700]

It turns out some projections stabilize faster than others. This log scaled plot shows the distances between substituent centers for all of our projections.

GeoListPlot[centroidPaths["LambertAzimuthal"], Joined -> True, ImageSize -> 700]

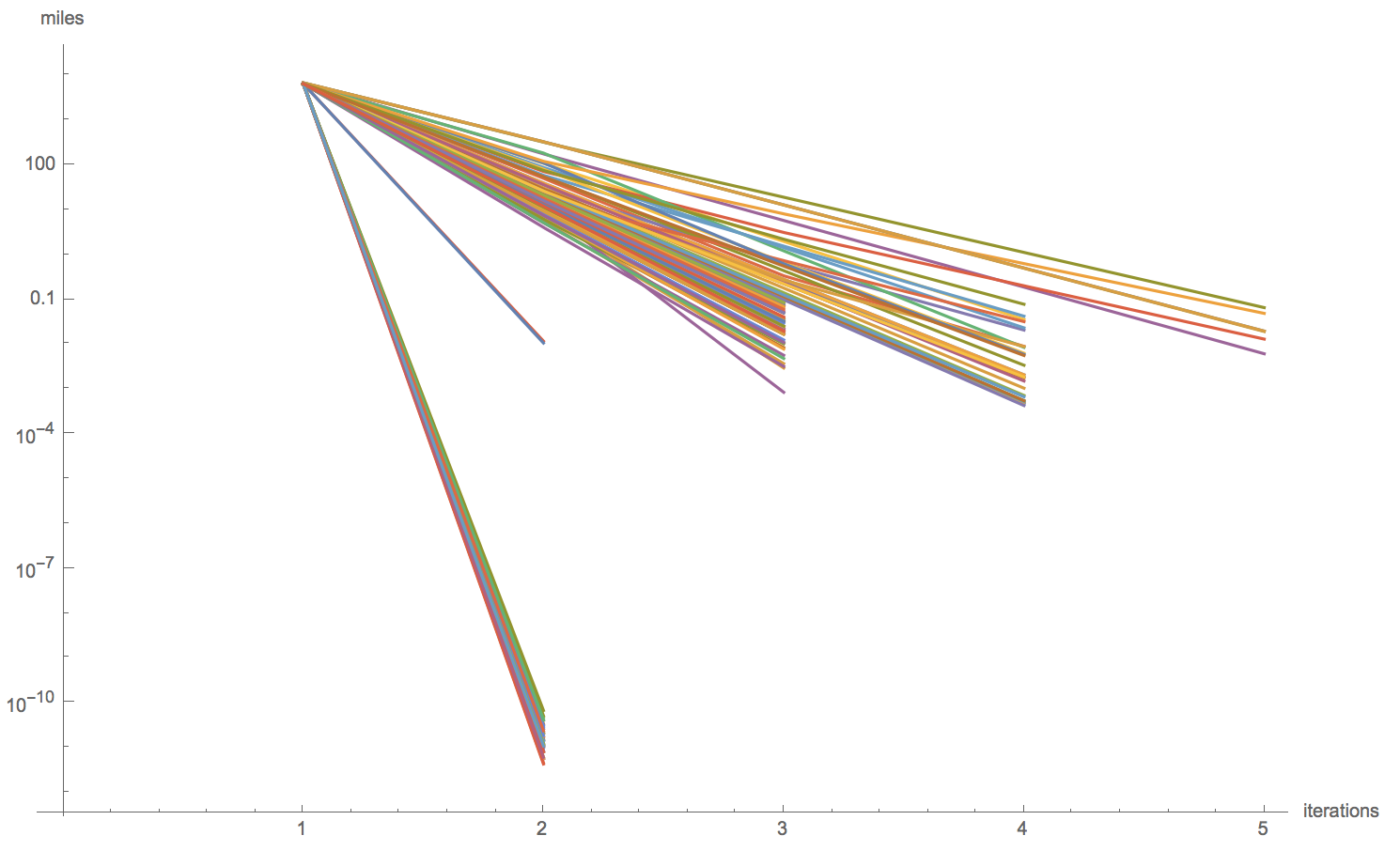
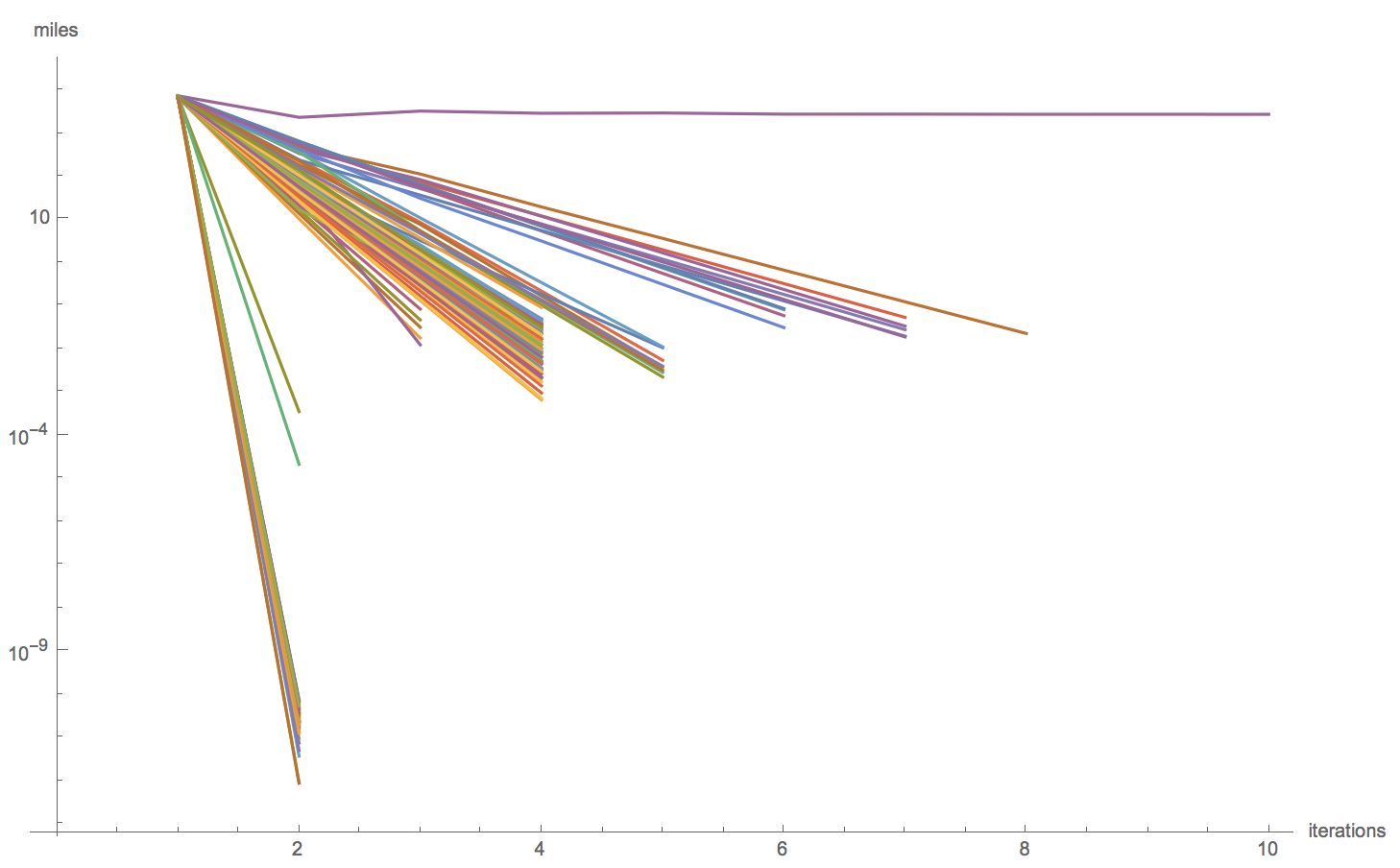
This is good, but we have to be a bit careful sometimes. For example, when including Alaska and Hawaii, a projection called "AugustEpicycloidal" never stabilizes. That's that purple line at the top of this next plot.

ListLogPlot[DeleteCases[Values[GeoDistanceList /@ DeleteMissing[centroidPaths, 2]], {}], Joined -> True, AxesLabel -> {"iterations", "miles"}]

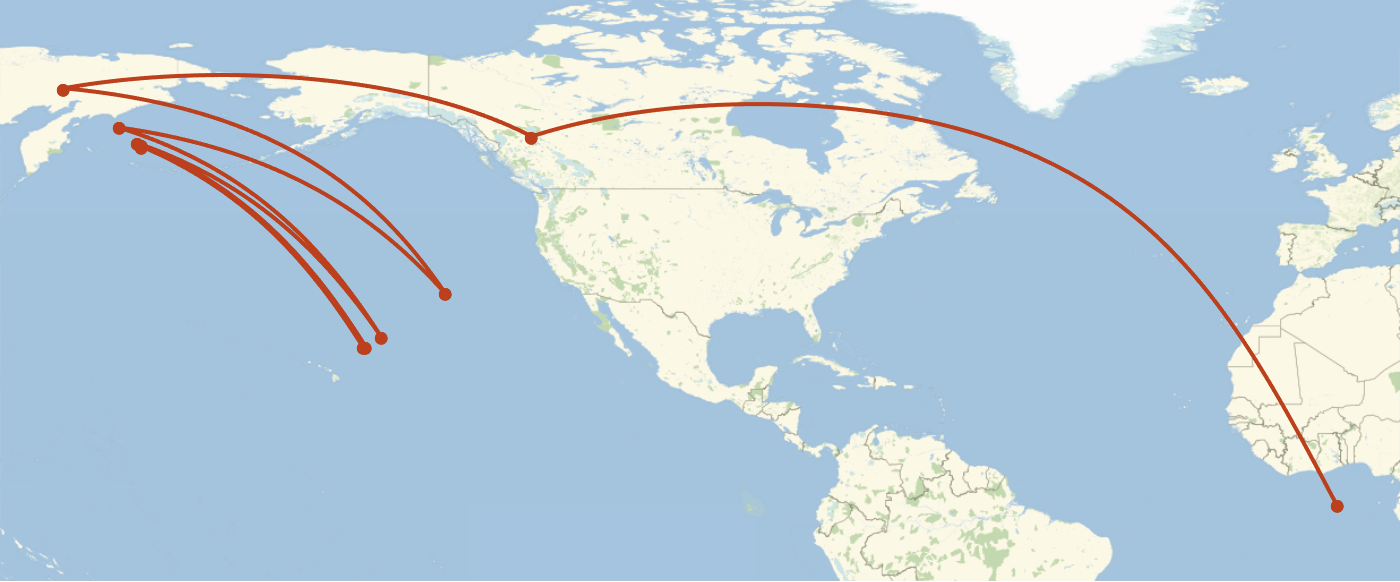
It turns out this projection bounces between two points in the Pacific forever.

GeoListPlot[centroidPaths["AugustEpicycloidal"], Joined -> True, ImageSize -> 700]

The points are far enough apart that we shouldn't just pick one, so we should just remove this projection when we include Alaska or Hawaii.

Finally, let's see the map for the centers calculated like this.

GeoListPlot[KeyValueMap[Labeled[#2, #1] &, DeleteMissing[centroids]], GeoRange -> "AdministrativeDivision", ImageSize -> 1000]

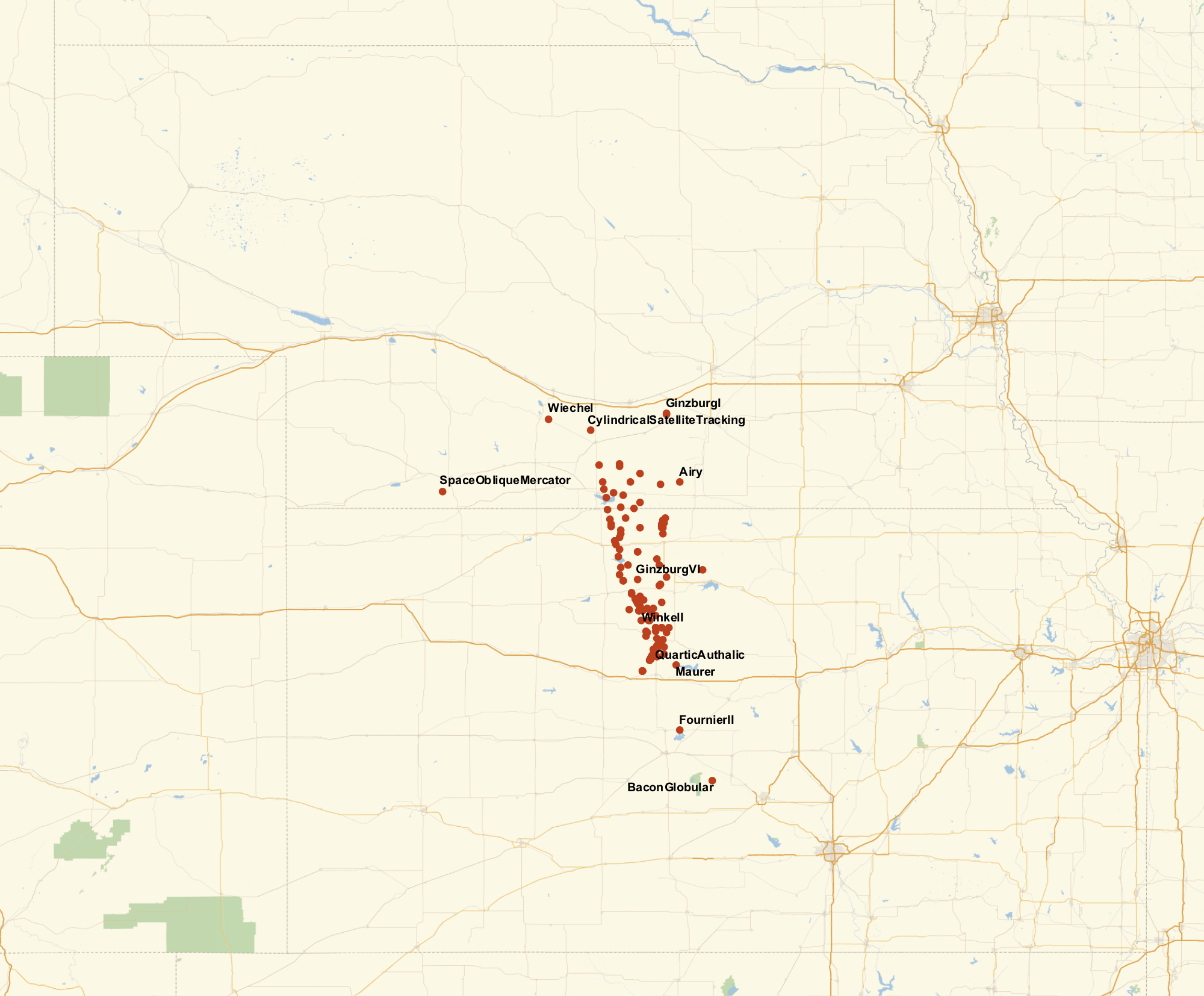
We get a much tighter clustering! This is nice, but it still doesn't give us a conclusive answer. There are some ways we could find the "center" (again, not well defined) of these points, but such a point would be in part determined by what projections we consider. Instead, we can look to some projection independent approaches.

Without Projections

3D Centroids

The first projection independent that comes to mind for me involves looking the region as an unprojected polygon in 3D. That is, get the shape of the US like an orange peel around the Earth. This is a handy function that uses GeoPositionXYZ to create such a shape.

countryRegion3D[meshI:(_MeshRegion|_BoundaryMeshRegion)] :=
    Block[{mesh = Quiet@TriangulateMesh@DiscretizeRegion@meshI},
        If[Head[mesh] =!= MeshRegion,
           Missing[],
           MeshRegion[GeoPositionXYZ[GeoPosition[Reverse/@MeshCoordinates[mesh]]][[1]], MeshCells[mesh,2]]
        ]
    ]

countryRegion3D[r]

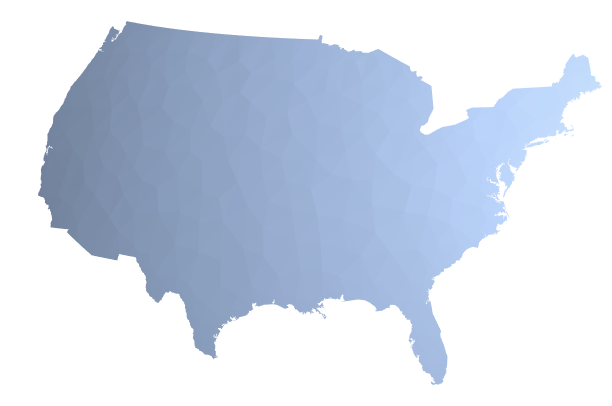
This is obviously projection independent. Now, to find the center of this, we can just find the centroid.

In[]:= RegionCentroid@countryRegion3D@r
Out[]= {-735688., -4.7425*10^6, 3.98579*10^6}

This centroid is in the coordinates of GeoPositionXYZ, so we can convert it back to a GeoPosition.

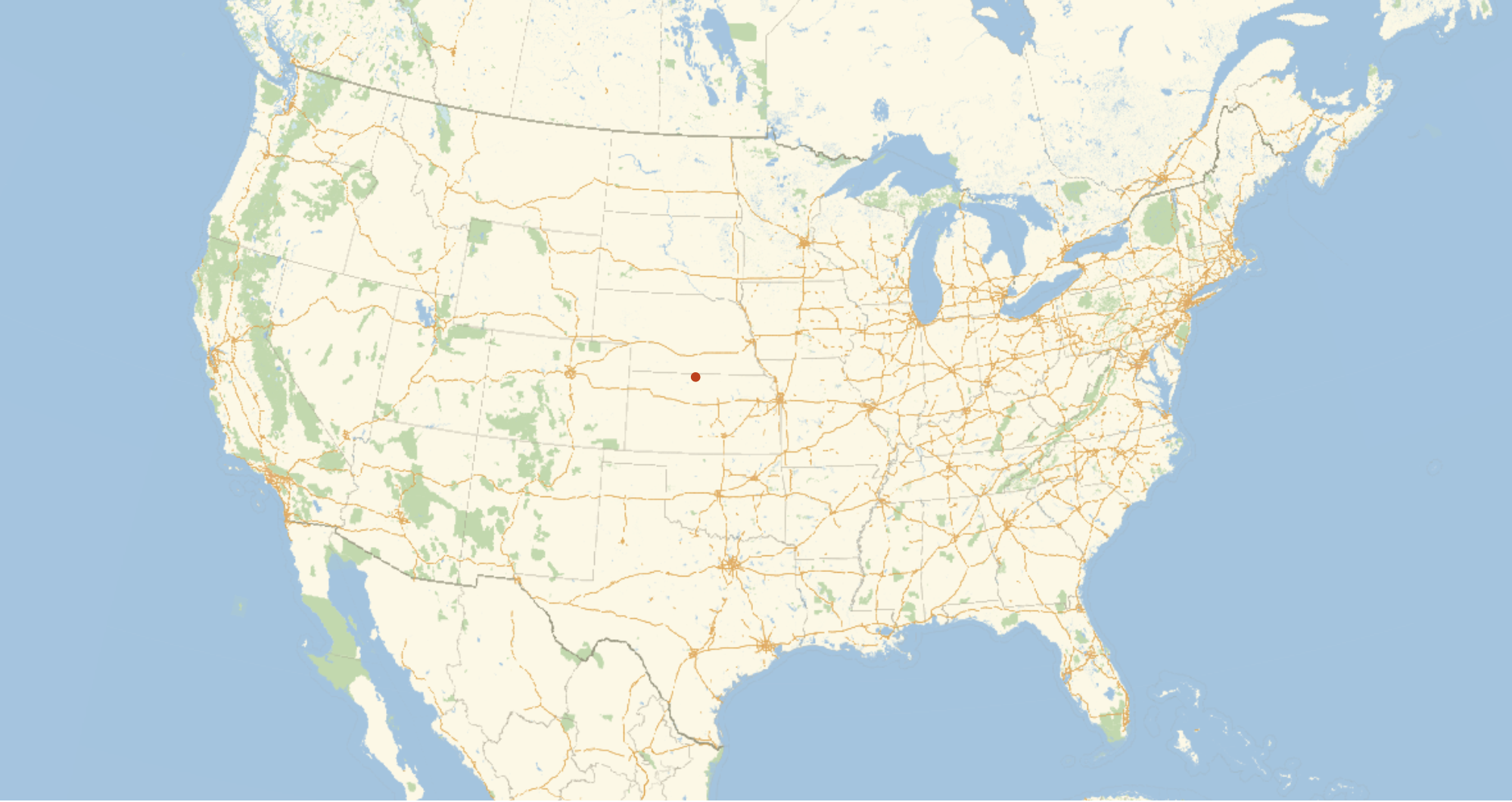
In[]:= GeoPosition@GeoPositionXYZ@RegionCentroid@countryRegion3D@r
Out[]= GeoPosition[{39.9031, -98.8178, -130866.}]

This point though is on the inside of the Earth. When we converted it back to a GeoPosition, we can see it has a third parameter. This parameter is the height, which in this case is negative (because it is inside the Earth). By ignoring that height, we are in essence drawing a line from the center of the Earth to that point and seeing where that line intersects the surface. This is what happens when we display this point with GeoListPlot.

GeoListPlot[GeoPosition@GeoPositionXYZ@RegionCentroid@countryRegion3D@r, GeoRange -> Entity["Country", "UnitedStates"], ImageSize -> 1000]

Median Coordinates

Oscar S. Adams suggests another approach before dismissing it. He suggests that you could find essentially the median latitude and longitude. That is, find the latitude such that if you cut the conterminous US along that latitude both resulting sides would have about the same area. The same operation could be performed with longitude.

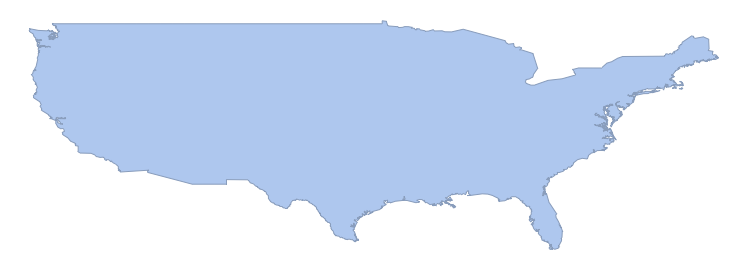
We have to be careful about how we do this because many projections don't preserve area, and many projections don't represents lines of latitude and longitude as straight horizontal and vertical lines. We can start then by projecting the region of interest into a projection that has these properties, "CylindricalEqualArea".

equalAreaR = projectMesh[r, "CylindricalEqualArea"]

We can now find the vertical and horizontal lines that cut this region into even halves.

clippedArea[r_, b_?NumberQ] := NIntegrate[Boole[x < b], {x, y} \[Element] r]

halfClipLocation[r_] := With[{targetArea = Area[r]/2}, NArgMin[Abs[clippedArea[r, b] - targetArea], {b, Sequence @@ RegionBounds[r][[1]]}]]

This finds the vertical line that cuts the conterminous US in half.

In[]:= medianX = halfClipLocation[equalAreaR]
Out[]= -98.0503

And this finds the horizontal line that cuts the conterminous US in half by essentially switching latitude and longitude and performing the same operation.

In[]:= medianY = halfClipLocation[MeshRegion[Reverse /@ MeshCoordinates@equalAreaR, MeshCells[equalAreaR, 2]]]
Out[]= 36.7212

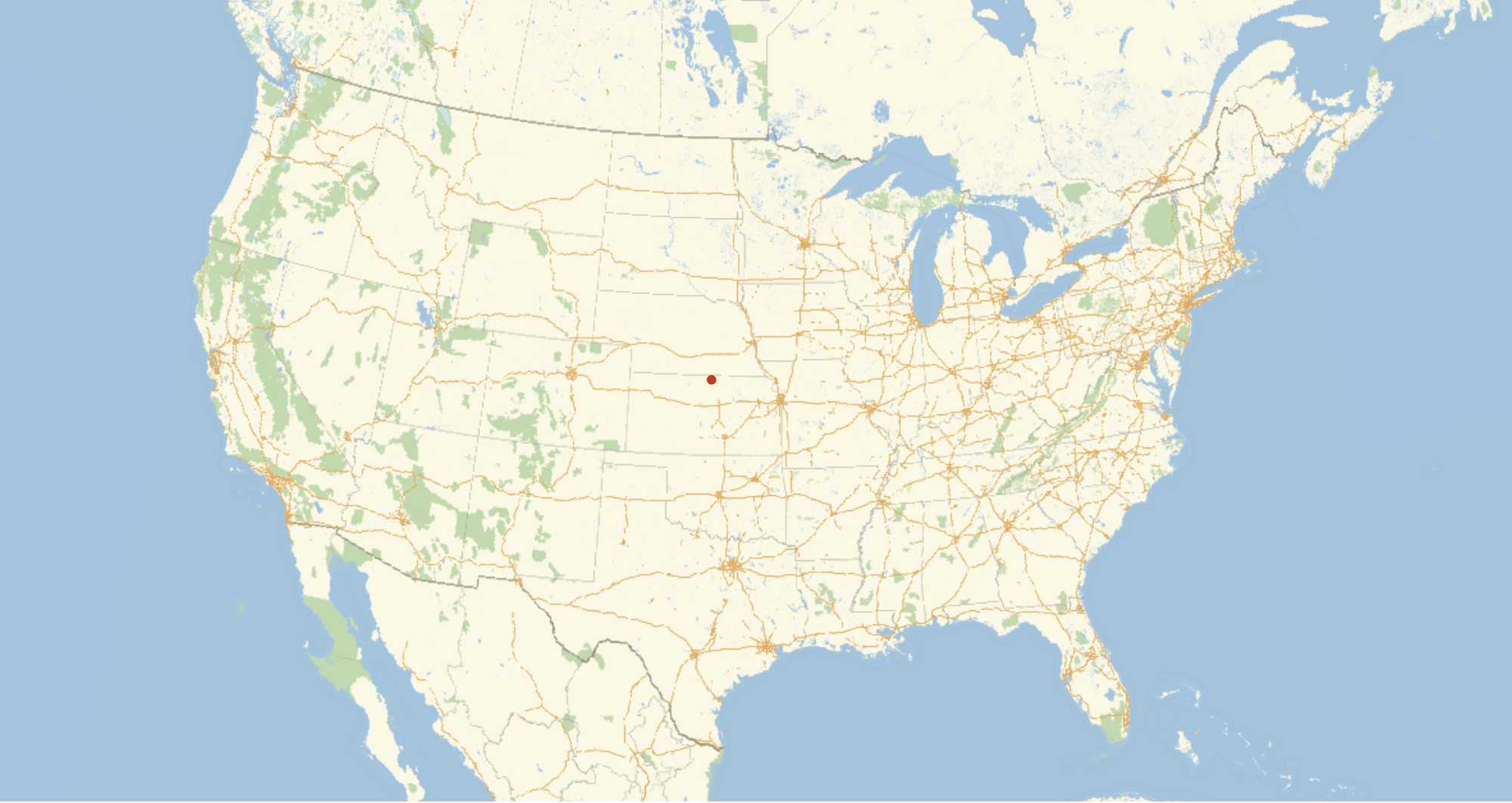
Now these numbers and in the coordinate system of the CylindricalEqualArea projection. We can use GeoGridPosition though to convert them into a GeoPosition.

In[]:= GeoPosition@GeoGridPosition[{medianX, medianY}, "CylindricalEqualArea"]
Out[]= GeoPosition[{39.8594, -98.0503}]

GeoListPlot[GeoPosition@GeoGridPosition[{medianX, medianY}, "CylindricalEqualArea"], GeoRange -> Entity["Country", "UnitedStates"], ImageSize -> 1000]

The problem with this, as Adams mentions, is that this isn't necessarily unique by the angle that you cut. That is, if instead of cutting along a line that runs north-south and another that runs east-west, you actually cut along lines shifted 45[Degree] from those, then you could get a different answer. That is, if the conterminous US was oriented differently on the globe, this method would give a different answer. If the conterminous US were rotated 45[Degree] and sitting in the middle of the pacific, the distance from this center point to, let's say, Chicago is not necessarily the same as if the conterminous US is where it actually is. This property seems undesirable because it depends on the orientation of the region on the earth when really the center seems like it should only be dependent on the shape of the region.

Central Features

There is one final method we will consider. This involves finding the central feature of the US. The central feature of a collection of points, as defined by the function conveniently named CentralFeature, is the point which minimizes the sum of the distances from each of those points to some central point. That is, it tries to find a point that is close to all the specified points. This is in many ways similar to the Riemannian center of mass, which is defined as being the same, but for the square of the distances. Now, we have a region and not a collection of points, so we need to use RandomPoint to get those points so that we can feed them to CentralFeature. CentralFeature already knows how to deal with GeoPositions, so this is all we have to do.

In[]:= centralFeature = CentralFeature@GeoPosition[Reverse /@ RandomPoint[r, 1000]]
Out[]= GeoPosition[{40.2308, -99.2463}]

Arguably, we really want to do this with an integral over the whole region instead of with some selected points, no matter how numerous, but realistically we would perform such an integral with Method->"MonteCarlo", and so this is not all too different. Here, we sampled the US with 1000 points. When put on a map, 1000 points seems to cover everything pretty well. However, this actually doesn't give consistent results.

features = Table[CentralFeature@GeoPosition[Reverse /@ RandomPoint[r, 1000]], 100];

GeoListPlot[features, GeoRange -> Entity["Country", "UnitedStates"], ImageSize -> 1000]

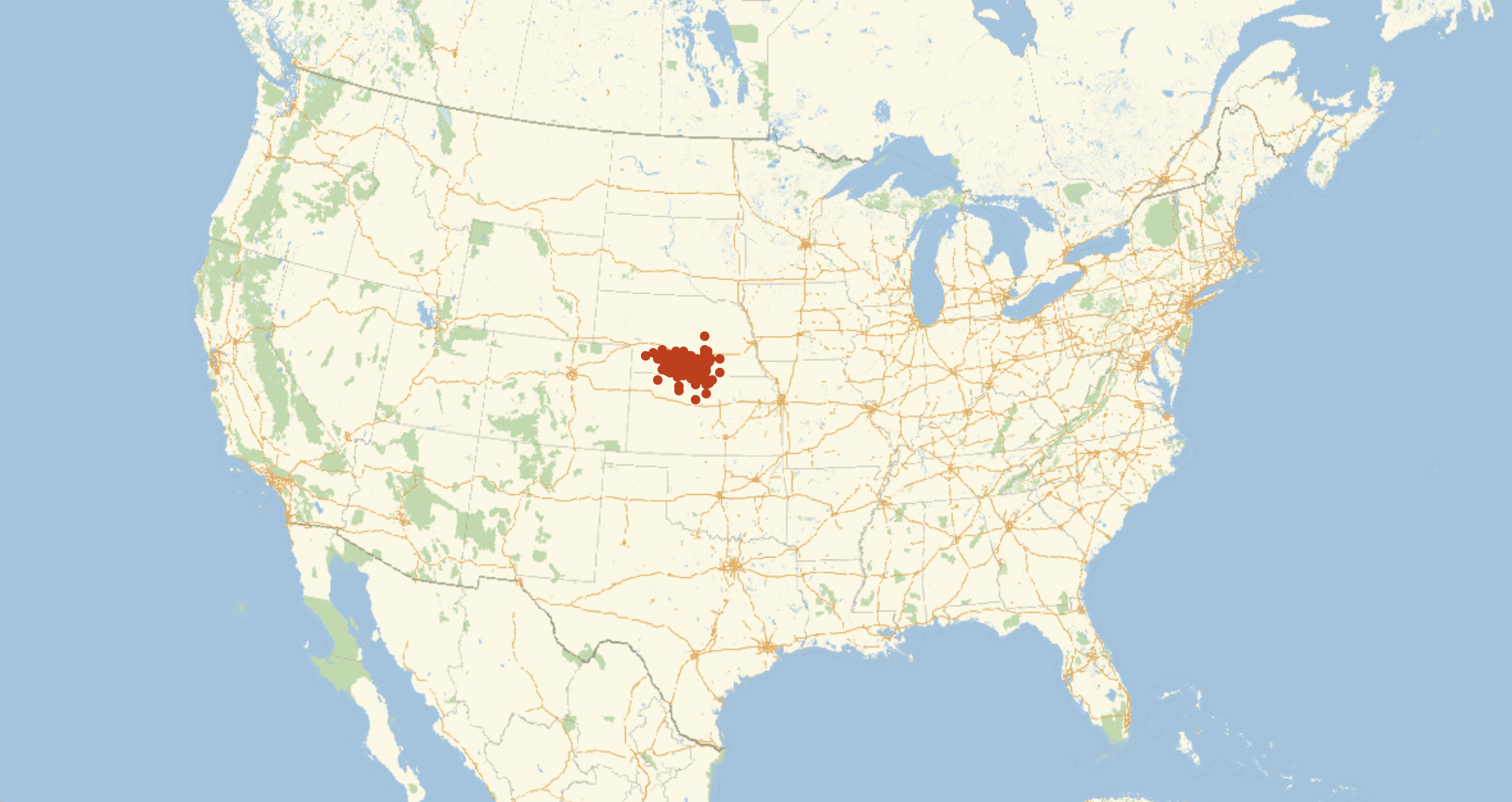
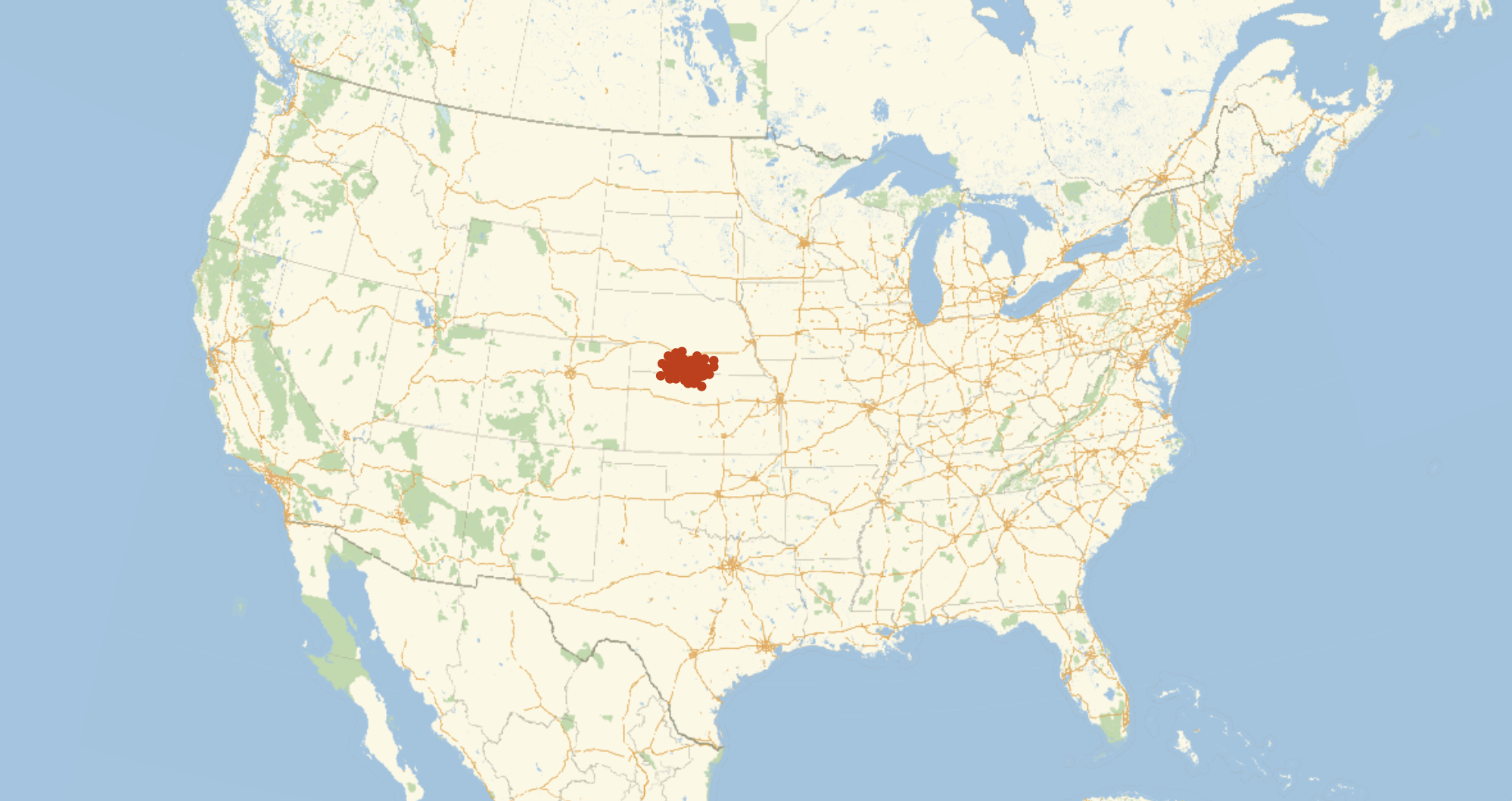
With 2000 points, it is more consistent, but still a rather large area.

features2 = Table[CentralFeature@GeoPosition[Reverse /@ RandomPoint[r, 2000]], 100];

GeoListPlot[features2, GeoRange -> Entity["Country", "UnitedStates"], ImageSize -> 1000]

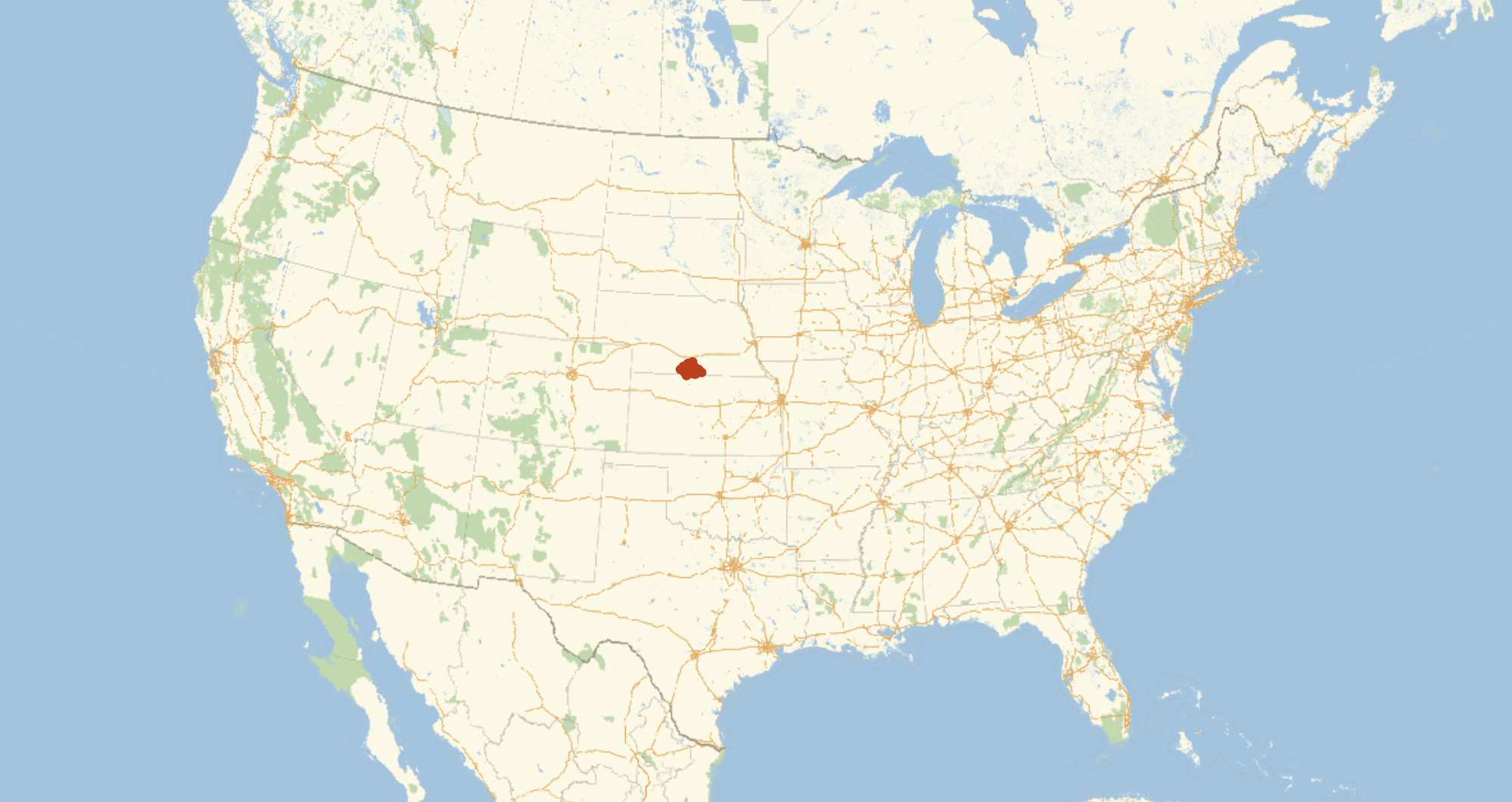
Overnight, I ran a similar computation with 15000 points. The clustering here is sufficient that any one of these points is fairly precise, but just for fun, we can take the CentralFeature of these to get a central point of our central points, and get a final center of the US.

features3 = Table[Echo@n; CentralFeature@GeoPosition[Reverse /@ RandomPoint[r, 15000]], {n, 100}];
features3 >> "~/Desktop/features3.wl";

GeoListPlot[features3, GeoRange -> Entity["Country", "UnitedStates"], ImageSize -> 1000]

GeoListPlot[features3, GeoRange -> "AdministrativeDivision", ImageSize -> 1000]

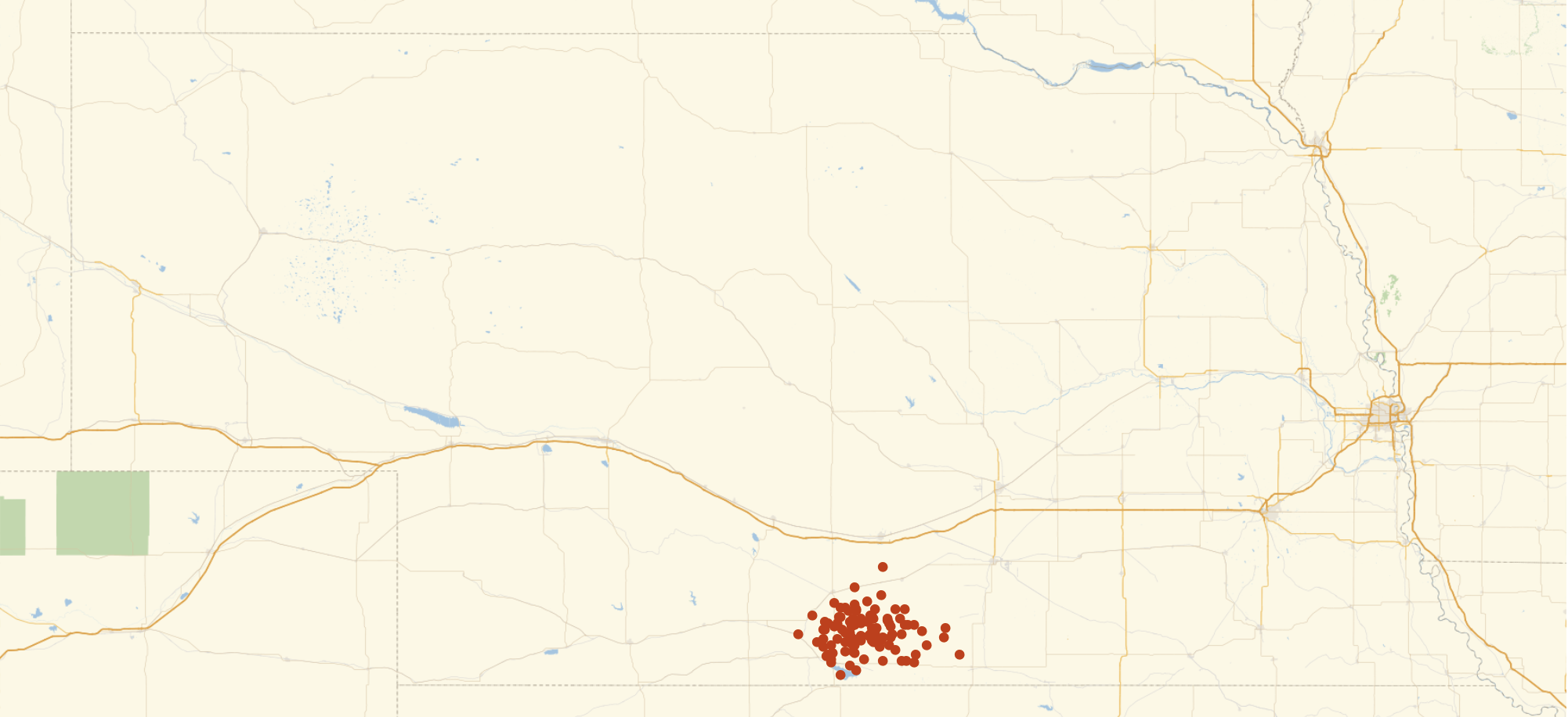
I personally find the method with the unprojected polygons most convincing. It is very easy and efficient to calculate a precise location, and that location is completely projection independent. The runner up for me is this CentralFeature method, but its complexity and the approximations that become necessary make it a bit harder to judge.

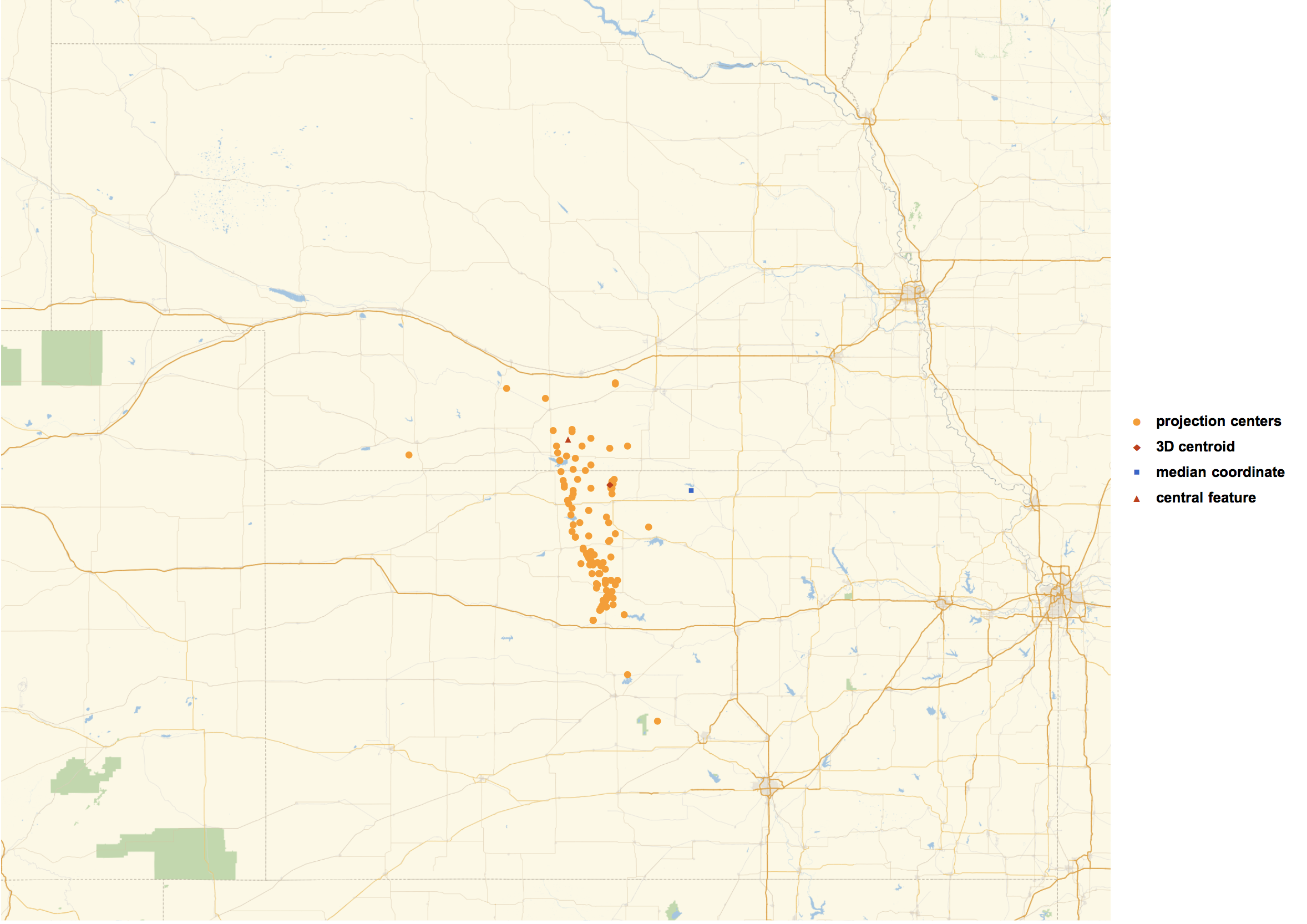
Finally, here is a map showing all of the centers of the conterminous US.

features3 = Get["~/Desktop/features3.wl"];
GeoListPlot[{
        Values@DeleteMissing[centroids],
        {GeoPosition@GeoPositionXYZ@RegionCentroid@countryRegion3D@r},
        {GeoPosition@GeoGridPosition[{medianX,medianY},"CylindricalEqualArea"]},
        {CentralFeature[features3]}},
    GeoRange->"AdministrativeDivision",ImageSize->1000,
    PlotLegends->{"projection centers","3D centroid","median coordinate","central feature"}]

Attachments: