Group Abstract Group Abstract

Message Boards Message Boards

[?] Plot function with two or more variables?

Mariana Melleu
Posted 9 years ago

Hey, guys! How are you?! I'm taking Calculus 3 classes and I'm having difficulties with functions of two or more variables. Of course the app shows the 3D form, but in class we have to represent this functions in the plane... and obviously we can't draw it with the same accurate of the app. So my question is: is there a way for Wolfram app to calculate the functions, plot the 3D graph, but also show the right way to graph in the plane? Thank you very much!
POSTED BY: Mariana Melleu
1 Reply
Sort By:
Brad Klee
Brad Klee
Posted 9 years ago

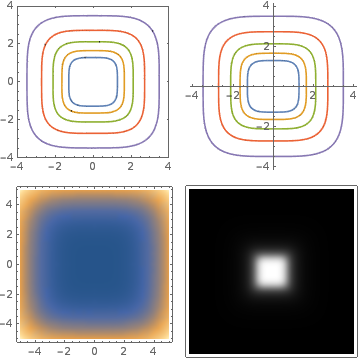
Hi Mariana, doing just okay. Trouble with calculus class... I think I know exactly what you are talking about, but hopefully no one is bothering you about any Weierstrass functions. Here are a few different in-plane plots 

g1 = ContourPlot[ Evaluate[x^4 + y^4 == Exp[#] & /@ Range[5]], {x, -5, 5}, {y, -5, 5}, PlotRange ->
{{-4, 4}, {-4, 4}}]
g2 = PolarPlot[ Evaluate[ r /. Solve[  Evaluate[
x^4 + y^4 /. {x -> r Cos[\[Theta]],   y -> r Sin[\[Theta]]}] == k, r][[1]] /. k -> Exp[#] & /@
Range[5]], {\[Theta], 0, 2 Pi},   PlotRange -> {{-4, 4}, {-4, 4}}];
g3 = DensityPlot[x^4 + y^4, {x, -5, 5}, {y, -5, 5}];
g4 = ArrayPlot@ Table[ArcTan[x^4 + y^4], {x, -5, 5, .01}, {y, -5, 5, .01}];

GraphicsGrid[{{ g1, g2 }, { g3 , g4 }}]

Squares

If you really look into it, everything in-plane can be drawn with Graphics:

Head /@ {g1, g2, g3, g4}
Out[]=  {Graphics, Graphics, Graphics, Graphics}

I think direct use of the Graphics function is the way to get highest quality results. Read The Function Manual!
POSTED BY: Brad Klee
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard