It is best to use NIntegrate in yours case.
f[a_?NumericQ, s_?NumericQ, g_?NumericQ] :=
NIntegrate[(Exp[-(x + s^2)/(2 a^2)]) (BesselI[0, Sqrt[x]*s/a^2]), {x,0, g}]
f[1., 2, 3]
(*0.580509*)
Analytical solution maybe not exist.
Integral represented by an infinite sum.
func = (Exp[-(x + s^2)/(2 a^2)]) (BesselI[0, Sqrt[x]*s/a^2])
sol = InverseZTransform[func /. x -> 1/x, x, n]
sol2 = Integrate[sol*x^n, {x, 0, g}, Assumptions -> n >= 0]
(*(2^-n a^(-2 n) E^(-(s^2/(2 a^2))) g^(1 + n) HypergeometricU[-n, 1, s^2/(2 a^2)])/((1 + n) Gamma[1 + n]^2)*)
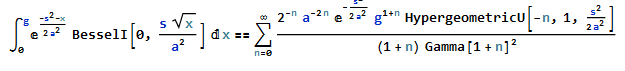
Sum[sol2, {n, 0, 1000}] /. a -> 1 /. s -> 2 /. g -> 3 // N
(*0.580509*)