Thanks Chris and Brad for your replies,

That is a lot of useful info, the eigenvector and value aspect is particularly useful, I thought it might be something along those lines but its been a good few years since I touched that stuff.

Just want to follow up on a few points. With the centroid command, does it average all the point data of the STL or actually compute the center of mass? For example if I have 2 faces of equal size yet one was divided into more triangular segments that biases the simple version of centroid that just considers just points and not an actual volume.

With the calculation of the moment of inertia tensor, I am trying to implement it myself in java so I am trying to work out the specific equations to use to turn the 3 points associated with an STL file facet and an origin (being also the center of mass) into the moment of inertia tensor.

Regarding an STL file example, I have only got simple primitives I've been testing my code on so-far where I know the answers already, such as rods around an axis, spheres, etc. The goal however is to take in 3D scan data of fruits and vegetables and have a consistent way to align them for comparing different species, such as length, width, volume, etc.

Hi Dan.

First, let's get a MeshRegion. We could use Import, but here I'm just going to use something from ExampleData.

r = DiscretizeGraphics[ExampleData[{"Geometry3D", "SedanCar"}]]

Next, it is easy to find the center of mass of this shape (assuming it is of uniform density). We can just use RegionCentroid.

In[]:= RegionCentroid[r]
Out[]= {-1.36011, 1.87744, 21.4279}

I believe that the axis around which this has the lowest moment of inertia is the eigenvector of the moment of inertia matrix with the lowest associated eigenvalue. We can compute that pretty easily, taking advantage of the fact that, according to its documentation page, "Eigenvectors with numeric eigenvalues are sorted in order of decreasing absolute value of their eigenvalues."

In[]:= Last[Eigenvectors[MomentOfInertia[r]]]
Out[]= {0.00163806, -0.999214, -0.0396081}

That should be the axis with the lowest moment of inertia. We can visualize all of this just to see if it is plausible.

Graphics3D[{
  EdgeForm[None], Opacity[0.2],
  MeshPrimitives[r, 2], 
  Opacity[1], Thick, Red, 
  InfiniteLine[RegionCentroid[r], Last[Eigenvectors[MomentOfInertia[r]]]],
  Blue, PointSize[Large], 
  Point[RegionCentroid[r]]}]

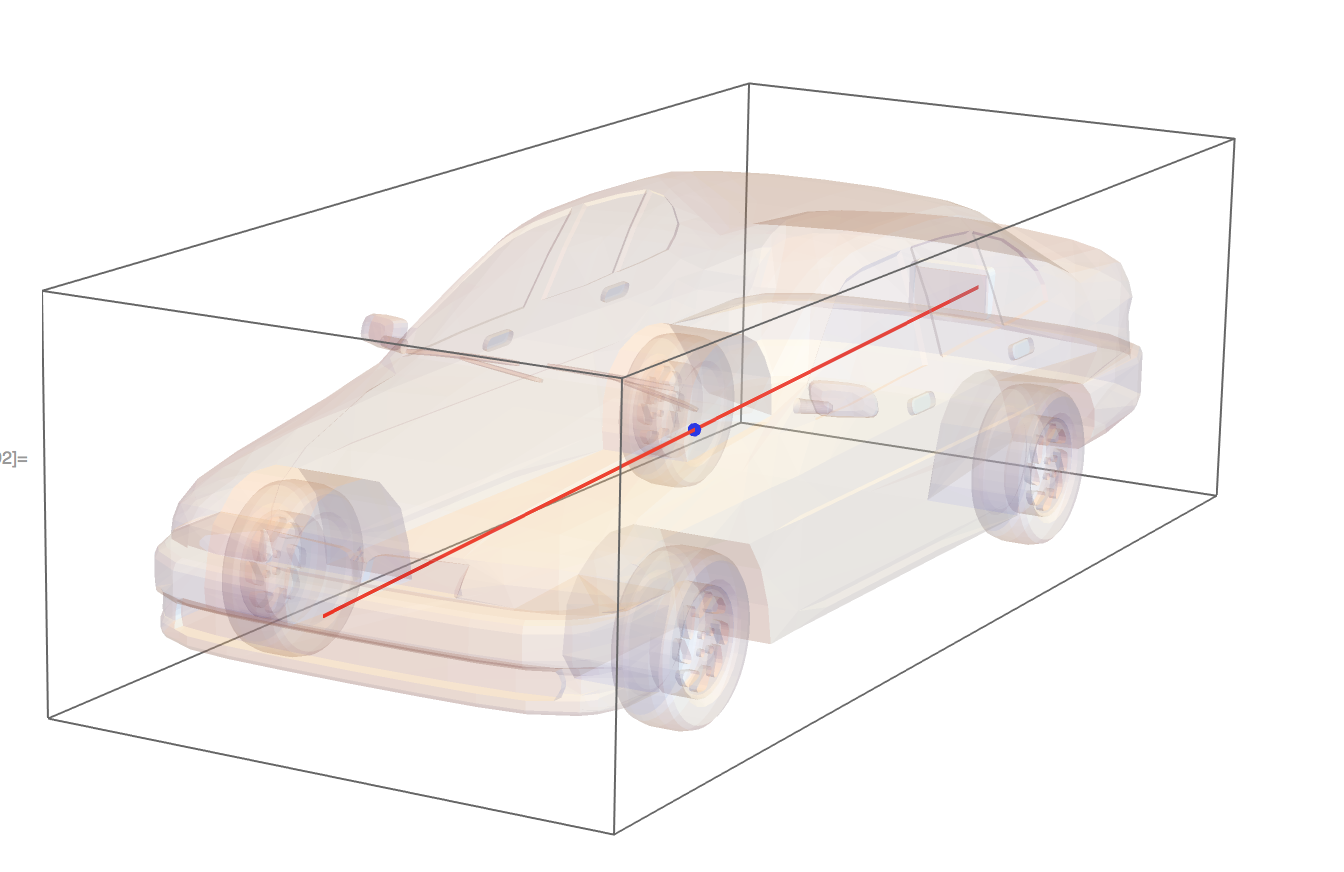
That looks plausible to me!

I hope that helps!