Group Abstract Group Abstract

Message Boards Message Boards

Image Correlation in Particle Image Velocimetry is behaving strangely

Note: i have posted the same question on MSE: https://mathematica.stackexchange.com/questions/148739/image-correlation-in-particle-image-velocimetry-is-behaving-strangely

I have been trying to implement a code for determining flow-field using Particle Image Velocimetry.

In this technique a user can take two images. Using small windows from the first image (which act as kernels) and search windows from the second image one can determine the cross-correlation which simply tells where the small window moves within a given search window. This process can be repeated between the second and the third image and so on.

A clear detail can be found in the second paragraph: http://www.physics.emory.edu/faculty/weeks//idl/piv.html

I have two images here (posting as a gif, you can save this and import it in mathematica as a list of two images): enter image description here

I use the following code to generate the flow-field.

windowsize = 32; (* select window size *)
imgDim = ImageDimensions[images[[1]]]; (* dimensions for the images *)
imgone = ImageCrop[images[[1]], imgDim - (2*windowsize)]; (* removing
border from first image: we dont want to create windows at the borders *)

firstimgsplits = ImagePartition[imgone, windowsize]; 
(* breaking the first image into small windows *)
searchwindows = ImagePartition[images[[2]], windowsize*3, {windowsize, windowsize}];
(* breaking the second image into search windows *)

{dim1, dim2} = Dimensions@searchwindows;
H = Last@ImageDimensions[imgone];

(* get midpoints of the windows of the first frame *)
midptsFirst = Flatten[Table[{i windowsize + windowsize/2, 
 j (windowsize) + windowsize/2}, {i, 1, dim1}, {j, 1, dim2}], 1];

(* pts in the second image where correlation is max *)
correlationPts = Table[MorphologicalComponents[ImagePad[
   ImageAdjust@ImageCorrelate[searchwindows[[i + 1, j + 1]], 
     firstimgsplits[[i + 1, j + 1]], NormalizedSquaredEuclideanDistance, 
     PerformanceGoal -> "Quality"], {{j*windowsize, H - windowsize (j + 1)},
{H - windowsize (i + 1), windowsize i}}, White]]~Position~0,
{i, 0, dim1 - 1}, {j, 0, dim2 - 1}]~Flatten~2;

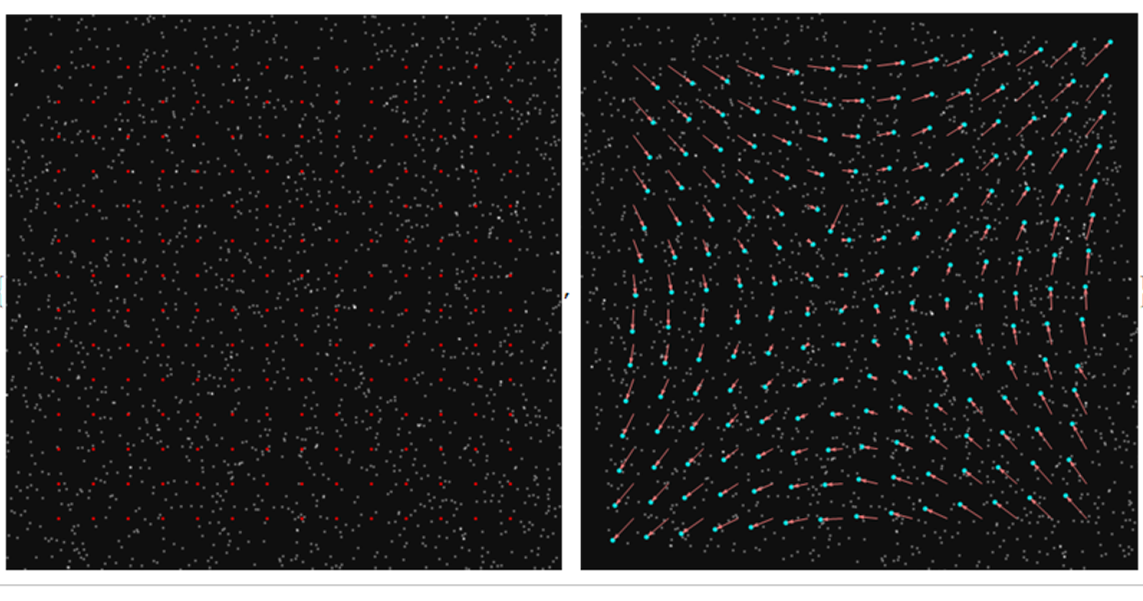
now when i create a flow-field from the displacement of points (red pts in the first image and cyan pts in second image) I can see that something is not right. My eyes tell me that the particles have move in a direction different from the ones found using ImageCorrelate

This should be rather straightforward for Mathematica. I do not know what is wrong in this simple piece of code. I will appreciate if someone can help me with this question.

ListAnimate@{Show[images[[1]], Graphics[{Red, Point@midptsFirst}]], 
Show[images[[2]], Graphics[{Cyan, PointSize[Medium], Point@correlationPts,
{Pink, Arrowheads[Small], MapThread[Arrow[{#1, #2}] &, {midptsFirst, correlationPts}]}}]]}

enter image description here

Attachments:
POSTED BY: Ali Hashmi
8 Replies
Sort By:

Hi Ali,

What commercial codes does is a bit more elaborate. Generally one uses multi-pass processing:

  1. For a course window (e.g. 128x128) one does the piv like you did. This will give you the rough motion for that area.
  2. Now one does the smaller scale: (64x64 or 32x32). But one does not compare the same pixels from each image; one already shifts the window by this approximate large-scale PIV. This will give much stronger correlation, because the overlap will be much larger.

This can be seen in your bottom-left, the displacement is large (~10-12 pixels i estimate) which is large fraction of your window. By selecting a windows that is roughly 10 pixels displaced already the correlation is much better.

In PIV one generally aims for 5-6 pixels displacement. Too small and one loses precision in determining the displacement. Too large and your windows need to be very large or many 'passes'.
POSTED BY: Sander Huisman

Hi Ali,

maybe I do not really understand your question, but is it not as simple as:

img = Binarize /@ Import["Testpiv3.gif"];
gtrf = Last[FindGeometricTransform @@ img];

Ready! -- Now one can do e.g.:

rpts = RandomInteger[{1, First@ImageDimensions[First@img]}, {1000, 2}];
Graphics[{Arrowheads[.01], Arrow /@ Transpose[{rpts, gtrf[rpts]}]}, ImageSize -> 600]

which gives:

enter image description here

Regards -- Henrik

POSTED BY: Henrik Schachner

Hi Henrik and Sander,

I have the code up on Github and mentioned you guys in the credits:

https://github.com/alihashmiii/simple-piv/blob/master/flowtrack.m
POSTED BY: Ali Hashmi

Hi Ali,

yes, I do think so: See documentation about FindGeometricTransform ->"Details and Options" -> TransformationClass.

Regards -- Henrik
POSTED BY: Henrik Schachner

Hi Henrik,

I had a a quick question. Will Geometric Transformation work in a complex case: for example, consider some particles in one region of the image rotate a little whereas particles in the second region of the image undergo a linear translation?

Regards, Ali
POSTED BY: Ali Hashmi

Also, I I think we should crop the image so that the edges are not taken into account during computation. But overall your procedure is way faster !! so thumbs up :)
POSTED BY: Ali Hashmi

Hi Henrik,

This is a very nice implementation. The advantage of using Mathematica is that solutions can be implemented using multiple approaches. Btw i have a little to offer to your code. We need to make sure that the points are in the image coordinate system. This was a mistake I made earlier when the flow-field looked queer. We can use a modified version of your code below:

images = Import["C:\\Users\\Ali Hashmi\\Desktop\\PIV\\Testpiv3.gif"];
imgDim = ImageDimensions[First@images];
windowsize = 32;
imgCorrD = First@imgDim;
img = ImageCrop[#, imgDim - (2*windowsize)] & /@ images; 
gtrf = Last[FindGeometricTransform @@ img];
rpts = RandomInteger[{windowsize, windowsize+First@ImageDimensions[First@img]}, {1000, 2}];
Graphics[{Arrowheads[.01], Darker@Cyan,  Arrow /@ Transpose[{Map[Abs[# - {0, imgCorrD}] &, #] &@rpts,
     Map[Abs[# - {0, imgCorrD}] &, #] &@gtrf[rpts]}]}, ImageSize -> 600]

enter image description here
POSTED BY: Ali Hashmi

Hi Sander,

I need time to understand what you mentioned in point #2.

Btw i think i found a mistake which atleast solves the issue. The position that are returned needs to be converted to image coordinate system. Silly mistake i would say.

See github code for the fix: https://github.com/alihashmiii/simple-piv/blob/master/flowtrack.m

enter image description here
POSTED BY: Ali Hashmi
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard