Message Boards Message Boards

0
|
4423 Views
|
1 Reply
|
0 Total Likes
View groups...
Share
Share this post:

Optimize computation time of Integrate[] ?

Juan Jose Garcia Ripoll, CSIC
Posted 8 years ago

Hi, I am doing some symbolic computation in a rather large notebook, but I find that Mathematica is underutilizing my computer resources. One bottleneck is the computation of

Efsoft = -(1/
     2) \[Nu]t - \[Alpha] Integrate[\[Nu] (\[Nu] + 
       2 \[Nu]t)/(\[Nu] + \[Nu]t)^2 Exp[-\[Nu]/\[Nu]c] Cos[
       2 \[Pi] \[Rho] \[Nu]]^2, {\[Nu], 0, \[Infinity]}];

The formula itself probably does not matter, but I see that Mathematica spends a lot of time and uses just 4% of the CPU of the system. Is this usual? I experience similar problems when running code with this copy of Mathematica 10, which has a campus license.
POSTED BY: Juan Jose Garcia Ripoll
1 Reply
Sort By:

If you solve indefine integral:

 sol = Integrate[? (? + 2 ?t)/(? + ?t)^2 Exp[-?/?c] Cos[2 ? ? ?]^2,v]
 sol2 = sol // Simplify 

 (* 1/4 (E^(-(?/?c) + 
      4 I ? ? ?) (?t^2/(? + ?t) + ?c/(-1 \
 + 4 I ? ?c ?)) + (
    E^(-? (1/?c + 
        4 I ? ?)) (I ? ?c + ?t (-I ?t + \
 ?c (I + 4 ? ?t ?))))/((? + ?t) (-I + 
       4 ? ?c ?)) + (
    2 E^(-(?/?c)) (?c (-? ?c + ?t (-?c + \
 ?t)) + 
       E^((? + ?t)/?c) ?t^2 (? + ?t) \
 ExpIntegralEi[-((? + ?t)/?c)]))/(?c (? + ?t)) \
 + (E^(?t (1/?c + 4 I ? ?)) ?t^2 (1 + 
       4 I ? ?c ?) ExpIntegralEi[-((
       I (? + ?t) (-I + 
          4 ? ?c ?))/?c)])/?c + (
    E^(?t (1/?c - 4 I ? ?)) ?t^2 (1 - 
       4 I ? ?c ?) ExpIntegralEi[(
      I (? + ?t) (I + 4 ? ?c ?))/?c])/?c)*)

and calculate limits with assumptions:

   Limit[sol2, ? -> 0, Assumptions -> {?t, ?c, ?} > 0]
  (*Complicated expression*)

The problem is Mathematica can't find this limit in infinity:

Limit[sol2, ? -> Infinity, Assumptions -> {?t, ?c, ?} > 0] = ?

Solution in Maple:

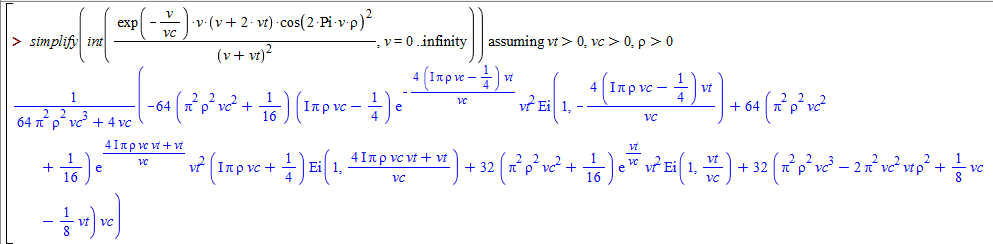
enter image description here

     (1/(4 (vc + 
        16 ?^2 vc^3 ?^2)))(4 vc (vc - vt + 
          8 ?^2 vc^2 (vc - 2 vt) ?^2) + 
       E^(vt (1/vc - 4 I ? ?))
         vt^2 (1 + 
          16 ?^2 vc^2 ?^2) (2 E^(4 I ? vt ?)
            ExpIntegralE[1, vt/
            vc] + (1 - 4 I ? vc ?) ExpIntegralE[1, 
            vt (1/vc - 4 I ? ?)] + 
          E^(8 I ? vt ?) (1 + 4 I ? vc ?) ExpIntegralE[1,
             vt (1/vc + 4 I ? ?)]))
POSTED BY: Mariusz Iwaniuk
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract