Note: i have posted the same question on MSE: https://mathematica.stackexchange.com/questions/148739/image-correlation-in-particle-image-velocimetry-is-behaving-strangely
I have been trying to implement a code for determining flow-field using Particle Image Velocimetry.
In this technique a user can take two images. Using small windows from the first image (which act as kernels) and search windows from the second image one can determine the cross-correlation which simply tells where the small window moves within a given search window. This process can be repeated between the second and the third image and so on.
A clear detail can be found in the second paragraph: http://www.physics.emory.edu/faculty/weeks//idl/piv.html
I have two images here (posting as a gif, you can save this and import it in mathematica as a list of two images): 
I use the following code to generate the flow-field.
windowsize = 32; (* select window size *)
imgDim = ImageDimensions[images[[1]]]; (* dimensions for the images *)
imgone = ImageCrop[images[[1]], imgDim - (2*windowsize)]; (* removing
border from first image: we dont want to create windows at the borders *)
firstimgsplits = ImagePartition[imgone, windowsize];
(* breaking the first image into small windows *)
searchwindows = ImagePartition[images[[2]], windowsize*3, {windowsize, windowsize}];
(* breaking the second image into search windows *)
{dim1, dim2} = Dimensions@searchwindows;
H = Last@ImageDimensions[imgone];
(* get midpoints of the windows of the first frame *)
midptsFirst = Flatten[Table[{i windowsize + windowsize/2,
j (windowsize) + windowsize/2}, {i, 1, dim1}, {j, 1, dim2}], 1];
(* pts in the second image where correlation is max *)
correlationPts = Table[MorphologicalComponents[ImagePad[
ImageAdjust@ImageCorrelate[searchwindows[[i + 1, j + 1]],
firstimgsplits[[i + 1, j + 1]], NormalizedSquaredEuclideanDistance,
PerformanceGoal -> "Quality"], {{j*windowsize, H - windowsize (j + 1)},
{H - windowsize (i + 1), windowsize i}}, White]]~Position~0,
{i, 0, dim1 - 1}, {j, 0, dim2 - 1}]~Flatten~2;
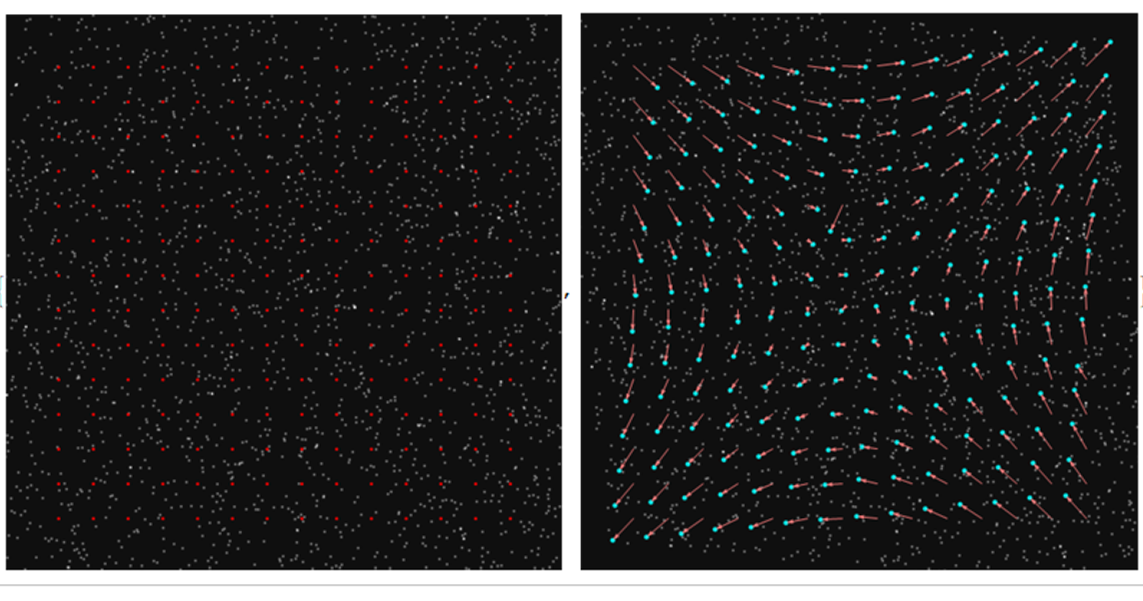
now when i create a flow-field from the displacement of points (red pts in the first image and cyan pts in second image) I can see that something is not right. My eyes tell me that the particles have move in a direction different from the ones found using ImageCorrelate
This should be rather straightforward for Mathematica. I do not know what is wrong in this simple piece of code. I will appreciate if someone can help me with this question.
ListAnimate@{Show[images[[1]], Graphics[{Red, Point@midptsFirst}]],
Show[images[[2]], Graphics[{Cyan, PointSize[Medium], Point@correlationPts,
{Pink, Arrowheads[Small], MapThread[Arrow[{#1, #2}] &, {midptsFirst, correlationPts}]}}]]}
 Attachments:
Attachments: