The function FindRoot can only find one root; there is no way of finding multiple roots. User J. M. extended the FindRoot by the function FindAllCrossings by changing Stan Wagon's book Mathematica in Action slightly.
The implementation is pretty slick. You plot the function on a certain range and tell the Plot function to mesh the zeros, then you extract the zeros and use FindRoot with them as an initial condition.
But this implementation has a major drawback; it fails in cases where the function doesn't cross zero, as x^2 for example.
To extend J. M. implementation I added some more lines of code, and I've made the code more verbose. The new lines of code calculate the zeros of the derivative of the function and then test it is close to zero and later refine it with FindRoot, this works even with functions as Abs[x], which has discontinuous derivative and never crosses zero, but thanks to the interpolated result, it takes care of that.
Options@FindRoots = Sort@Join[Options@FindRoot, {MaxRecursion -> Automatic, PerformanceGoal :> $PerformanceGoal, PlotPoints -> Automatic, Debug -> False, ZeroTolerance -> 10^-2}];
FindRoots[fun_, {var_, min_, max_}, opts:OptionsPattern[]] := Module[{PlotRules, RootRules, g, g2, pts, pts2, lpts, F, sol},
(* Extract the Options *)
PlotRules = Sequence @@ FilterRules[Join[{opts}, Options@FindRoots], Options@Plot];
RootRules = Sequence @@ FilterRules[Join[{opts}, Options@FindRoots], Options@FindRoot];
(* Plot the function and "mesh" the point with y-coordinate 0 *)
g = Normal@Plot[fun, {var, min, max}, MeshFunctions -> (#2 &), Mesh -> {{0}}, Method -> Automatic, Evaluate@PlotRules];
(* Get the meshes zeros *)
pts = Cases[g, Point[p_] :> SetPrecision[p[[1]], OptionValue@WorkingPrecision], Infinity];
(* Get all plot points *)
lpts = Join@@Cases[g, Line[p_] :> SetPrecision[p, OptionValue@WorkingPrecision], Infinity];
(* Derive the interpolated data to find other zeros *)
F = Interpolation[lpts, InterpolationOrder->2];
g2 = Normal@Plot[Evaluate@D[F@var, var], {var, min, max}, MeshFunctions -> (#2 &), Mesh -> {{0}}, Method -> Automatic, Evaluate@PlotRules];
(* Get the meshes zeros and retain only small ones *)
pts2 = Cases[g2, Point[p_] :> SetPrecision[p[[1]], OptionValue@WorkingPrecision], Infinity];
pts2 = Select[pts2, Abs[F@#] < OptionValue@ZeroTolerance &];
pts = Join[pts, pts2]; (* Join all zeros *)
(* Refine zeros by passing each point through FindRoot *)
If[Length@pts > 0,
pts = Map[FindRoot[fun, {var, #}, Evaluate@RootRules]&, pts];
sol = Union@Select[pts, min <= Last@Last@# <= max &];
(* For debug purposes *)
If[OptionValue@Debug, Print@Show[g, Graphics@{PointSize@0.02, Red, Point[{var, fun} /. sol]}]];
sol
,
If[OptionValue@Debug, Print@g];
{}
]
]
Example:
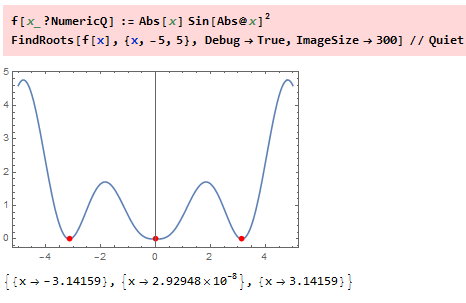
My primary use of this function is to find the eigenvalues of dielectric waveguides. They are found as the zeros of the boundary conditions.