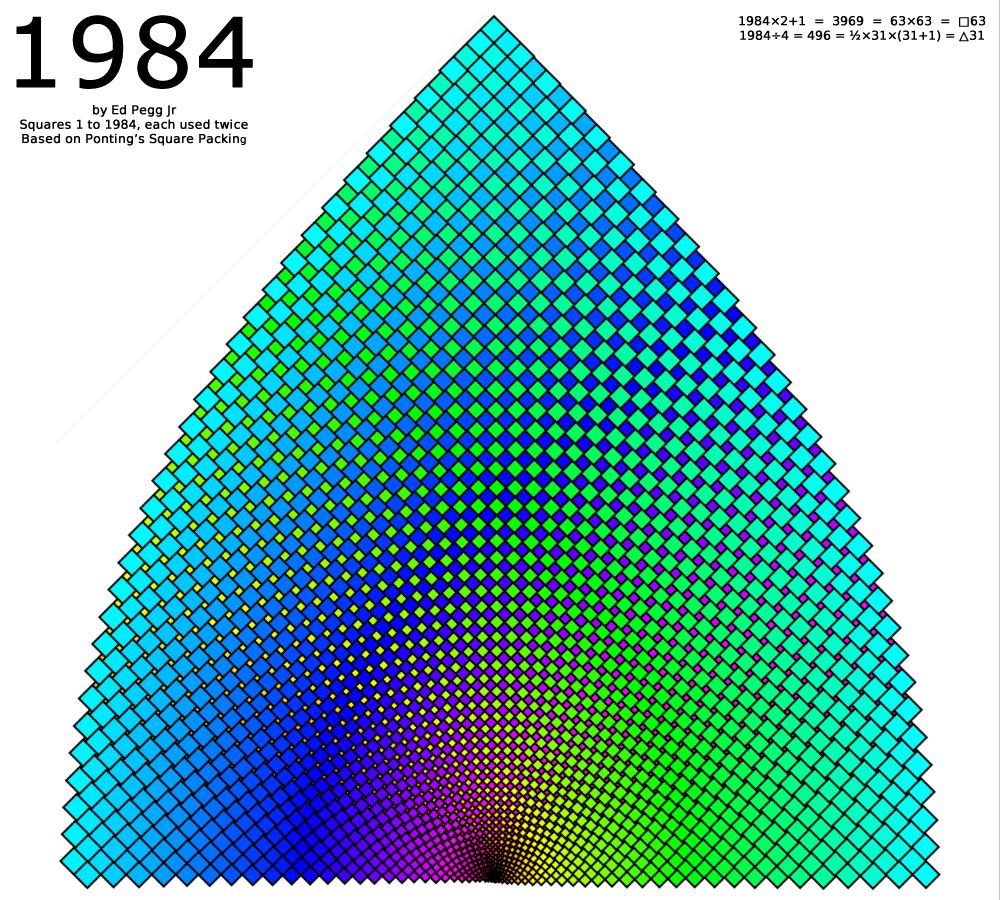
The Demonstration Ponting Square Packing can arrange sequentially sized squares into an asymmetric shape. I've often wondered if the method could be used to obtain symmetry.
Turns out that subtracting half gives half a lune. For the below I started with an arrangement of 19^2 = 361 squares, then subtracted 181. That gives a half lune where all squares of size 1 to 180 are represented twice. Make another copy and the 720 squares (four copies of squares 1 to 180) will make a lune.

I suppose it's actually a lens.
I figured out that curve, mostly. It's a hyperbola. I still haven't figured out the optimal way to fit the two pieces together with a unifying curve. But here's a stab at it.
squarepoly[{corner_, size_}] := Table[corner, {4}] + {{0, 0}, {0, size}, {size, size}, {size, 0}};
pontingMatrix[order_Integer] := Reverse[Reverse /@ (Partition[Reverse[If[IntegerQ[#], #, 0] & /@ (#/2 + 1/2 & /@
Range[(2 order + 1)^2])], (2 order + 1)] +Reverse /@ Transpose[Partition[
If[IntegerQ[#], # + ((2 order + 1)^2 + 1)/2, 0] & /@ (#/2 & /@Range[(2 order + 1)^2]), (2 order + 1)]])];
Module[{pm, xx, yy, alt, r1n, rn1, rad, numbers, squares1, squares2,
offset1, offset2, siz, order, count},
siz = 31;
order = (2 siz + 1);
count = (order^2 - 1)/2;
pm = pontingMatrix[siz] - (count + 1);
numbers = False;
xx = 2 siz + 1; yy = 2 siz + 1;
alt = Flatten[Append[Table[{1, -1}, {siz}], 1]];
r1n = Transpose[{FoldList[Plus, 0, Drop[ pm[[1]], -1]],Drop[Flatten[{#, #} & /@ (First /@
Partition[Append[FoldList[Plus, 0, Drop[alt pm[[1]], -1]], 0], 2])], 1]}];
rn1 = Transpose[{Drop[Flatten[{#, #} & /@ (First /@ Partition[
Append[FoldList[Plus, 0, Drop[alt, -1] Drop[ Transpose[pm][[1]], 1]], 0], 2])], -1],
FoldList[Plus, 0, Drop[ Transpose[pm][[1]], -1]]}];
rad = Table[If[Min[{a, b}] == 1, {0, 0},
If[OddQ[a + b], {0, pm[[a - 1, b]]}, {pm[[a, b - 1]], 0}]], {a, 1,xx}, {b, 1, yy}];
rad[[1, 1]] = {0, 0};
Do[rad[[1, nn]] = r1n[[nn]]; rad[[nn, 1]] = rn1[[nn]], {nn, 2, xx}];
Do[If[OddQ[a + b], rad[[a, b]] = rad[[a - 1, b]] + rad[[a, b]],
rad[[a, b]] = rad[[a, b - 1]] + rad[[a, b]]], {a, 2, xx}, {b, 2, yy}];
offset1 = {88650, 0} - (squarepoly[{rad[[1, 63]], pm[[1, 63]]}].N[RotationMatrix[-78/100 - Pi/2]])[[3]];
offset2 = {-88650, 0} - (squarepoly[{rad[[1, 63]], pm[[1, 63]]}].N[RotationMatrix[-78/100 + Pi/2]])[[3]];
squares1 = Table[{Hue[.3 + Abs[pm[[a, b]]]/count], Polygon[(# + offset1 & /@ (squarepoly[{rad[[a, b]], pm[[a, b]]}].N[
RotationMatrix[-78/100 - Pi/2]]))]}, {a, 1, xx}, {b, 1, yy}];
squares2 = Table[{Hue[.3 + Abs[pm[[a, b]]]/count], Polygon[# + offset2 & /@ (squarepoly[{rad[[a, b]], pm[[a, b]]}].N[
RotationMatrix[-78/100 + Pi/2]])]}, {a, 1, xx}, {b, 1, yy}];
Graphics[{EdgeForm[{Black, Thin}], squares1, squares2,
Plot[45200 - 5.04953`*^-17 x - 5.64864`*^-6 x^2, {x, -89316.1`, 89316.1}, PlotStyle -> {Thickness[0.003], Darker[Gray]}][[1]],
Plot[-45200 + 5.04953`*^-17 x + 5.64864`*^-6 x^2, {x, -89316.1, 89316.1}, PlotStyle -> {Thickness[0.003], Darker[Gray]}[[1]]},
ImageSize -> {1200, 600}]]
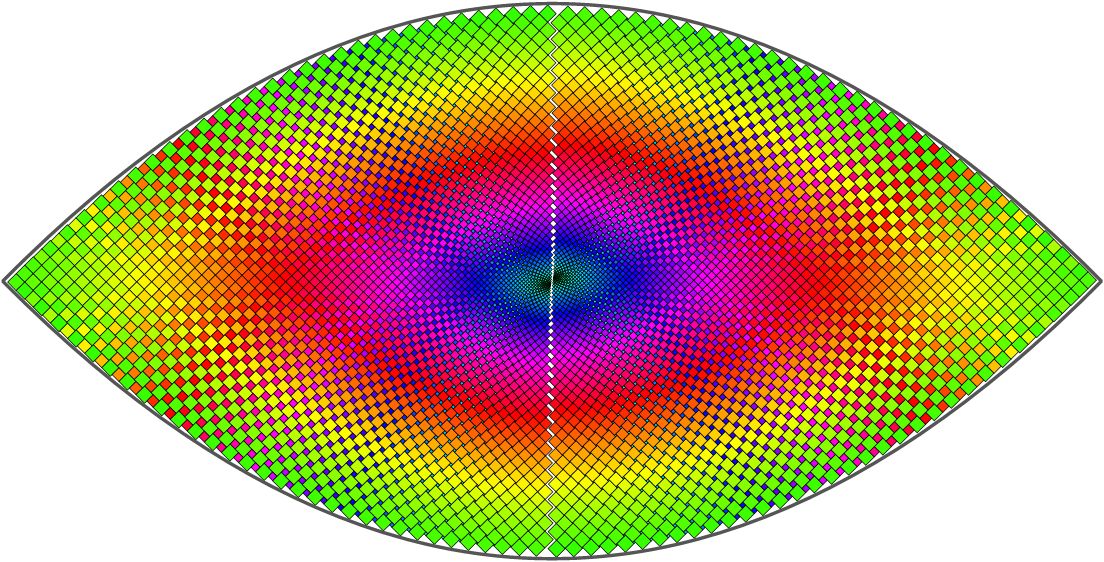
There should be a way to recursively optimize the (rotation, fit, offsets) for the hyperbolas. After that, clashing squares in the middle could be moved to voids near the hyperbolas, then more recursion.