Saleh,

I would do it all in a Dynamic Module. Using loops and inputs is not very Mathematica-like.

Here is an example:

DynamicModule[{M = 100, sols, n, beam = 1},
 sols = \[CapitalOmega] /. 
   Table[FindRoot[
     Tanh[Sqrt[\[CapitalOmega]]] - 
      Tan[Sqrt[\[CapitalOmega]]], {\[CapitalOmega], IG}], {IG, 10, 
     200, 50}];
 f[x_, n_] := 
  Sum[sols[[n]]^(2 i)/(4 i + 2)! x^(4 i + 2), {i, 0, M}] - 
   Sum[sols[[n]]^(2 i)/(4 i + 2)!, {i, 0, M}]/
     Sum[sols[[n]]^(2 i)/(4 i + 3)!, {i, 0, M}] Sum[
     sols[[n]]^(2 i)/(4 i + 3)! x^(4 i + 3), {i, 0, M}];
 Panel[Column[{Row[{"Single-Span:", 
      PopupMenu[
       Dynamic[beam], {1 -> "Free-Pinned", 2 -> "Clamped-Free"}], 
      Row[{"Mode:", SetterBar[Dynamic[n], Range[Length[sols]]]}]}],
    Dynamic[Plot[f[x, n], {x, 0, 1}, ImageSize -> Large]]}]]]

Which gives you a dynamic like this:

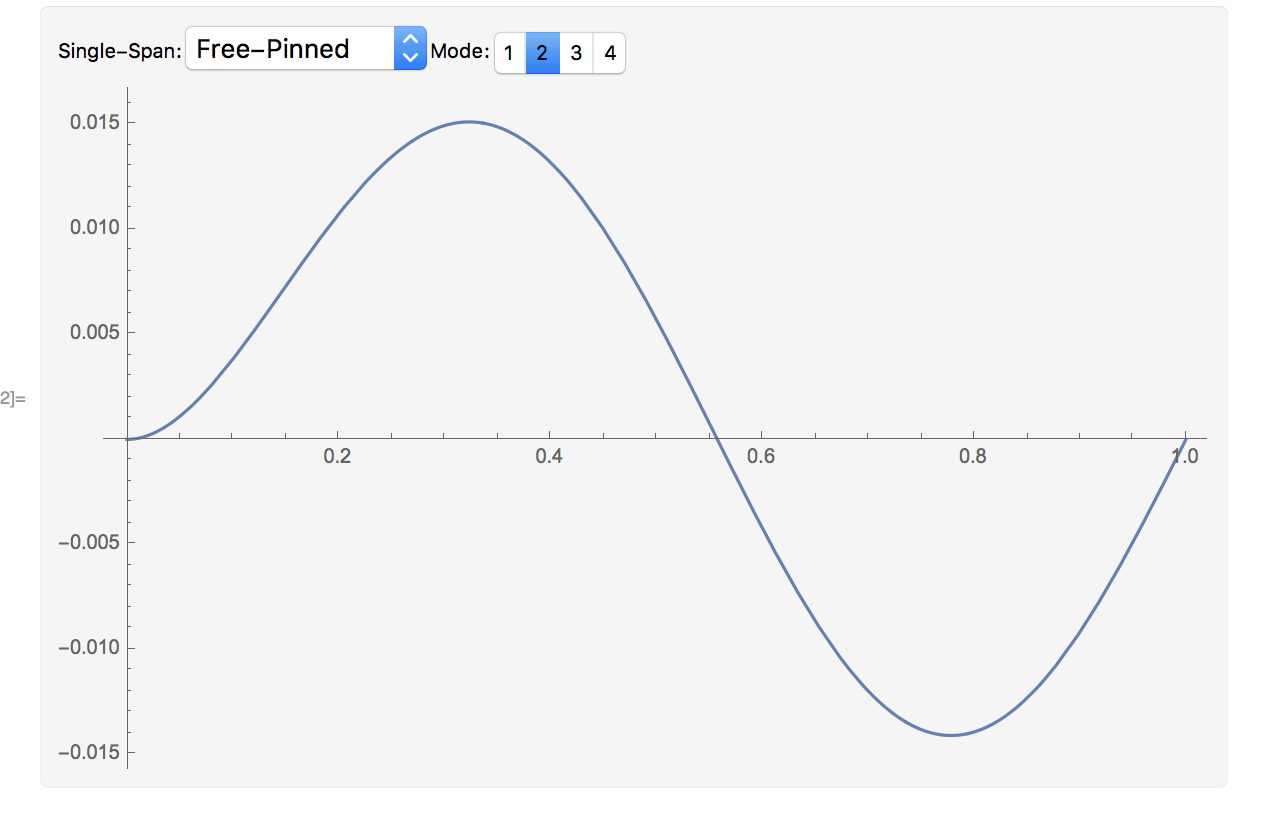
The SetterBar can be made to automatically resize based on how many modes there are in the solution. I obviously did not add any functionality to the beam type popup but you can do that. Use the dynamic variable "beam" to change your solution so the plot will change.

Regards,

Neil

Perhaps

ClearAll["Global`*"];
M = 100;
sols = ? /. Table[FindRoot[Tanh[Sqrt[?]] - Tan[Sqrt[?]], {?, IG}], {IG, 10, 200, 50}];
f[x_, n_] := Sum[sols[[n]]^(2 i)/(4 i+2)! x^(4 i+2), {i,0,M}] - Sum[sols[[n]]^(2 i)/(4 i+2)!, {i,0,M}]/
     Sum[sols[[n]]^(2 i)/(4 i+3)!, {i,0,M}] Sum[sols[[n]]^(2 i)/(4 i+3)! x^(4 i+3), {i,0,M}];
n = Input["which mode do you want?"];
Plot[f[x, n], {x, 0, 1}]

The error in your error is in red.