The area of a unit-edge triangle is $\sqrt3/4$. The volume of a unit-edge tetrahedron is $1/(6\sqrt2)$. What happens beyond that? At the entry simplex we can find the Cayley-Menger Determinant. Since all those $d$ values will be 1, we end up taking the determinant of the inverse of the identity matrix. So we end up with reciprocals of the following for dimensions 2 to 6.
1/Table[Sqrt[(-1)^(n + 1)/(2^n (n!)^2) MatrixForm[(1 - IdentityMatrix[n + 2])]], {n, 2, 6}]
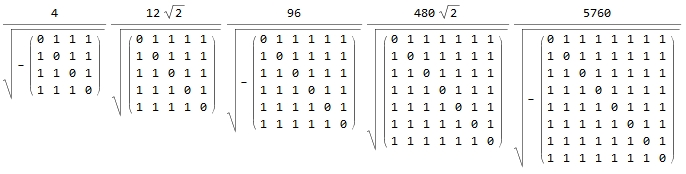
The bottom (actually top) part winds up being $\sqrt{3},\sqrt{4},\sqrt{5},\sqrt{6},\sqrt{7}$ for dimensions 2 to 6, or dimension+1. The top (actually bottom) part is $\sqrt{2^n} n!$. The volume of the $n$-simplex turns out to be ${\large \frac{\sqrt{2^n} n!}{\sqrt{n+1}}}$.
Table[Sqrt[n + 1]/(Sqrt[2]^n n!), {n, 2, 12}]
It seems that the reciprocals of dimensions 7 and 8 seem to be integers. The code below finds the sequence A155946: 7, 8, 17, 24, 31, 48, 49, 71, 80, 97, ... .
First /@ Select[Table[{n, (Sqrt[2]^n n!)/Sqrt[n + 1]}, {n, 2, 1000}], IntegerQ[Last[#]] &]
For another check, (16) at Triangle Area and (1) at Tetrahedron suggests a sequence of matrices that appends 1 to each coordinate and takes the determinant. If all but one of the coordinates is some permutation of $\left(0,0,0, ..., \frac{1}{\sqrt{2}} \right)$, those $n-1$ edges will all be distance 1 from each other. For the last coordinate point, we can find a point $\left( a,a,a, ..., a \right)$ at distance 1 from the other points.
FullSimplify[(a /. Solve[Sqrt[(n - 1) a^2 + (a - 1/Sqrt[2])^2] == 1, a]) ]
That gives us $a$ values of $ \frac{1-\sqrt{n+1}}{n\sqrt{2}}$ or $\frac{1+ \sqrt{n+1}}{n\sqrt{2}} $. For dimension 4, the former value is $\frac{1-\sqrt{5}}{4 \sqrt{2}} = \frac{\sqrt{3-\sqrt{5}}}{-4} = \frac{1-\phi }{\sqrt8}$, where $\phi$ is the golden ratio. That leads to the following matrix which happens to give the predicted volume.
$${\small V = \frac{\sqrt5 }{96} = \frac{1}{4!} \left| \begin{matrix} 0 & 0 & 0 & \frac{1}{\sqrt{2}} & 1 \\\\ 0 & 0 & \frac{1}{\sqrt{2}} & 0 & 1 \\\\ 0 & \frac{1}{\sqrt{2}} & 0 & 0 & 1 \\\\ \frac{1}{\sqrt{2}} & 0 & 0 & 0 & 1 \\\\ \frac{1-\phi }{\sqrt8} & \frac{1-\phi }{\sqrt8} & \frac{1-\phi }{\sqrt8} & \frac{1-\phi }{\sqrt8} & 1 \\\\ \end{matrix} \right| }$$
The square, cube, hypercube and so on are easier to calculate.