There are curious discretization artifacts:

ContourPlot[x^2 == 1/10000, {x, -1, 1}, {y, -1, 1}, 
 PlotRange -> {{.0022, .01}, {-.3, .3}}]
ContourPlot[10000 x^2 == 1, {x, -1, 1}, {y, -1, 1}, 
 PlotRange -> {{.0022, .01}, {-.3, .3}}]

Also, in the current Mathematica version the tooltip looks like a job left incomplete.

And one more additional curiosity:

ContourPlot[x^2 == 1/10000, {x, -1, 1}, {y, -1, 1}, PlotRange -> {{.0022, .01}, {-.3, .3}}, PlotPoints -> 30]
ContourPlot[10000 x^2 == 1, {x, -1, 1}, {y, -1, 1}, PlotRange -> {{.0022, .01}, {-.3, .3}}, PlotPoints -> 30]

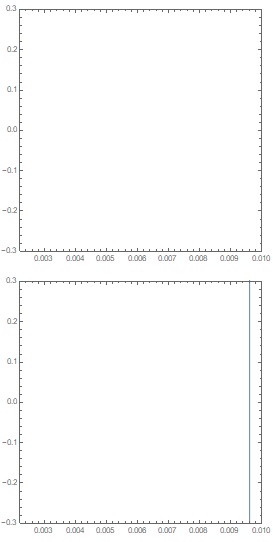
Why are not identical the results?

The numerical algorithms of ContourPlot assume nonzero derivative, or transversality, otherwise they may fail spectacularly:

ContourPlot[x^2 == 0, {x, -1, 1}, {y, 0, 1}]

In your case you get a correct plot by symbolic pre-processing:

ContourPlot[
 Evaluate[List @@ 
   Reduce[Cos[2*x]^2 == 0 && -Pi/2 < x < Pi/2, x, Reals]],
 {x, -Pi/2, Pi/2}, {y, 0, 2 Pi}]

It's interesting that the graph may be obtain if the right part is not exactly $0$:

ContourPlot[
 Cos[2 x]^2 == 0.000000000000000001, {x, -\[Pi]/2, \[Pi]/2}, {y, 0, 
  2 \[Pi]}]