I'm not sure what is confusing about .99 being less than .999, or what that might have to do with taking a limit (which is what I had asked). I will add that the entire thread has been remarkably murky in terms of stating what exactly is wanted and what exactly has been tried. Let me comment on some related issues that I believe are being raised.
(1) Precision in a plot range. The input shown in an earlier post does not produce a plot (this fact, and the error message, should have been noted in that post).
ff = ((1 + b)^2)/Sqrt[1 - b^2]
LogLogPlot[ff, {b, .9999999999999999999, .99999999999999999999}]
(* During evaluation of In[122]:= Plot::plld: Endpoints for b in {b,0.9999999999999999999,0.99999999999999999999} must have distinct machine-precision numerical values.
Out[122]= LogLogPlot[ff, {b, 0.9999999999999999999,
0.99999999999999999999}] *)
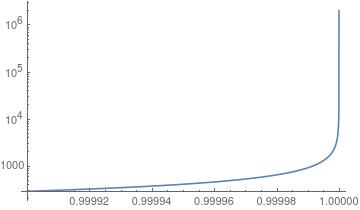
What to do about it? One remedy is to widen the range. You can let the right bound be 1 for example. This next will give a picture that might be informative.
LogLogPlot[ff, {b, .9999, 1}, PlotRange -> All]
(2) Solving runs into precision problems. This can be alleviated by explicitly using higher precision in the input. Notice the back-tic in the input below. It parses the input number to 20 digits precision.
Solve[ff - .99999999999999`20 == 0, b]
(* Out[111]= {{b -> -5.00000000000006875*10^-15}} *)
(3) More confusion. If the interest is in b approaching 1, that's not the same thing as ff being close to 1. So the use of Solve seems unhelpful for the stated problem (as best I can interpret it). I would guess what is wanted is for ff to be large and then find b. This requires considerable precision, roughly twice as many digits in for the number you want out. Some analysis of the expression might help to explain this (e.g. expand in Puisiux series centered at b=1). Anyway, here is an example. Notice the decimal point is at the right rather than left side of the value for ff.
NSolve[ff - 99999999999999999999.`40 == 0, b]
(* Out[139]= {{b -> 0.9999999999999999999999999999999999999992}} *)