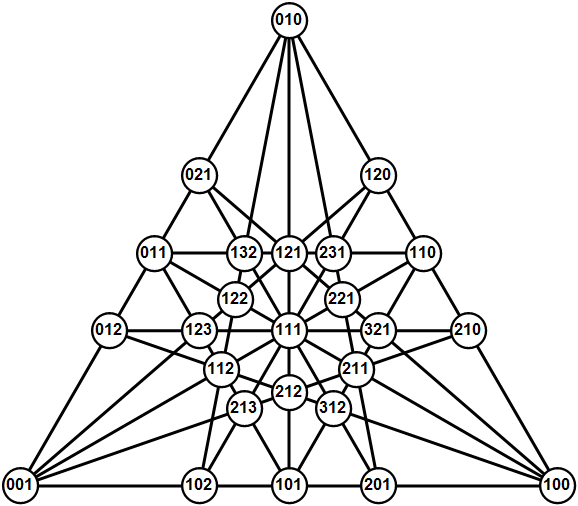
At Extreme Orchards for Gardner I mentioned barycentric coordinates. I found an interesting connection between the terms of degree 0 1 2 3 and barycentrics for record-setting lines in 3D space. The power set has the ab terms of degree 0 to 3. I calculate points of permutations of this power set. By appending 1 to each, the points can be gathered into lines with RowReduce. And then the graphic, showing how 64 points can be arranged in 66 lines of 4 points.
powerset ={{0, 0, 0, 1}, {0, 0, a, b}, {0, a^2, a b, b^2}, {a^3, a^2 b, a b^2, b^3}};
tetra = {{-1, -1, -1}, {-1, 1, 1}, {1, -1, 1}, {1, 1, -1}};
FromBarycentrics[{m_, n_, o_, p_}, {{x1_, y1_, z1_}, {x2_, y2_, z2_}, {x3_, y3_, z3_}, {x4_, y4_, z4_}}] := {m x1 + n x2 + o x3 + (1 - m - n - o) x4, m y1 + n y2 + o y3 + (1 - m - n - o) y4, m z1 + n z2 + o z3 + (1 - m - n - o) z4};
pts = Sort[FromBarycentrics[#/Total[#], tetra] & /@ Flatten[Permutations[#] & /@ (powerset /. {a -> 5, b -> 9}), 1]];
lines = Select[Union[Flatten[#, 1]] & /@ SplitBy[SortBy[Subsets[Append[#, 1] & /@ pts, {2}], RowReduce], RowReduce], Length[#] == 4 &];
lindex = Flatten[Position[pts, Drop[#, -1]] & /@ #] & /@ lines;
Graphics3D[{Sphere[#, .092] & /@ pts, Tube[pts[[#]], .02] & /@ lindex}, SphericalRegion -> True, Boxed -> False, ImageSize -> 800]
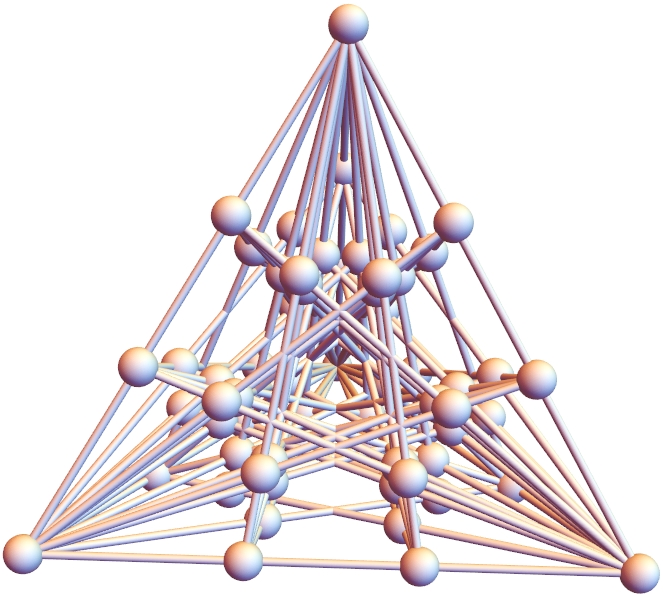
In above, I use $a=5, b=9$, but any reasonable values work. 0001 0011 0111 1111 1122 1112 1222 0012 0112 0122 1123 1223 1233 0123 2345 can be used instead to produce 241 lines of 5, a sporadic 3D extension of my previous graphic.