This idea came from my need to demonstrate a simple physical phenomenon such as the motion of a spring mass system to my undergraduate students. In the absence of a live demo, built-in Wolfram Language functions such as Animate and Manipulate come in handy. Here I will try to show a few simple examples.

In order to set up a stationary spring-mass system where the spring is tied to a fixed wall on one side and a mobile block on the other end, I used a simple graphics setup as follows:

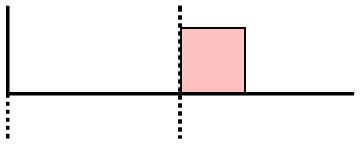
Graphics[{Thickness[0.01], Line[{{0, 1}, {0, 0}, {4, 0}}], {Dashed, Line[{{x, 1}, {x, 0}, {x, -0.5}}], 
            Line[{{2, 1}, {2, 0}, {2, -0.5}}], Line[{{0, 0}, {0, -0.5}}]}, {EdgeForm[Thick], Pink, Opacity[0.5], 
                                                                              Rectangle[{x + .01, 0.01}, {x + 0.76, 0.76}]}}]

ListLinePlot[Table[{(x - 0.19)/3900 i + 0.1 (1 - Cos[\[Pi]/100 (i - 1)]), 0.36 + 0.1 Sin[\[Pi]/100 (i - 1)]}, {i, 1, 3901}], 
                               AspectRatio -> 1, PlotStyle -> Black, Axes -> False]

Show[Graphics[{Thickness[0.01], Line[{{0, 1}, {0, 0}, {4, 0}}], 
             {Arrowheads[0.03], Thickness[0.005], Arrow[{{0.8, -0.15}, {0, -0.15}}], Arrow[{{1, -0.15}, {2, -0.15}}], 
                Text[Style["\!\(\*SubscriptBox[\(x\), \(0\)]\)", FontSize -> 30], {0.9, -0.15}], 
                    If[x > 2.3 \[Or] x < 1.7, {Arrowheads[{-0.03, 0.03}], Arrow[{{2, -0.3}, {x, -0.3}}], 
                                                               Text[Style["x", FontSize -> 30], {0.5 x + 1, -0.45}]}], 
             {Red, Arrow[{{x, 0.85}, {2, 0.85}}], Text[Style["F = - k x", FontSize -> 30], {2, 1.1}]}, 
             {Dashed, Line[{{x, 1}, {x, 0}, {x, -0.5}}], Line[{{2, 1}, {2, 0}, {2, -0.5}}], Line[{{0, 0}, {0, -0.5}}]}}, 
             {EdgeForm[Thick], Pink, Opacity[0.5], Rectangle[{x + .01, 0.01}, {x + 0.76, 0.76}]}}],
         ListLinePlot[Table[{(x - 0.19)/3900 i + 0.1 (1 - Cos[\[Pi]/100 (i - 1)]), 0.36 + 0.1 Sin[\[Pi]/100 (i - 1)]}, 
                              {i, 1, 3901}], 
         AspectRatio -> 1, PlotStyle -> Black, Axes -> False], PlotRange -> {{0, 4}, {-0.7, 1.5}}]

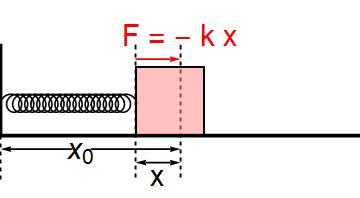
In the above figure I have also added more information using Text[] ...

Now we are at a position to animate the above figure and see if what we get.

Animate[Show[Graphics[{Thickness[0.01], Line[{{0, 1}, {0, 0}, {4, 0}}], 
                 {Arrowheads[0.03], Thickness[0.005], Arrow[{{0.8, -0.15}, {0, -0.15}}], Arrow[{{1, -0.15}, {2, -0.15}}], 
                     Text[Style["\!\(\*SubscriptBox[\(x\), \(0\)]\)", FontSize -> 30], {0.9, -0.15}], 
                      If[x > 2.3 \[Or] x < 1.7, {Arrowheads[{-0.03, 0.03}], Arrow[{{2, -0.3}, {x, -0.3}}], 
       Text[Style["x", FontSize -> 30], {0.5 x + 1, -0.45}]}], {Red, Arrow[{{x, 0.85}, {2, 0.85}}], 
      Text[Style["F = - k x", FontSize -> 30], {2, 1.1}]},
                    {Dashed, Line[{{x, 1}, {x, 0}, {x, -0.5}}], Line[{{2, 1}, {2, 0}, {2, -0.5}}], Line[{{0, 0}, {0, -0.5}}]}}, 
      {EdgeForm[Thick], Pink, Opacity[0.5], Rectangle[{x + .01, 0.01}, {x + 0.76, 0.76}]}}], 
             ListLinePlot[Table[{(x - 0.19)/3900 i + 0.1 (1 - Cos[\[Pi]/100 (i - 1)]),  0.36 + 0.1 Sin[\[Pi]/100 (i - 1)]}, 
                                      {i, 1, 3901}], AspectRatio -> 1, PlotStyle -> Black, Axes -> False], 
                     PlotRange -> {{0, 4}, {-0.7, 1.5}}], {x, 1, 3}, AnimationRunning -> False, AnimationRepetitions -> 2,                            AnimationDirection -> ForwardBackward]

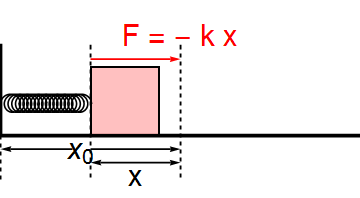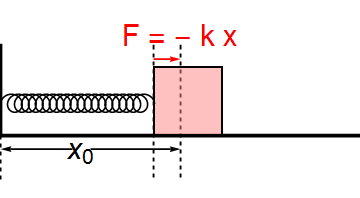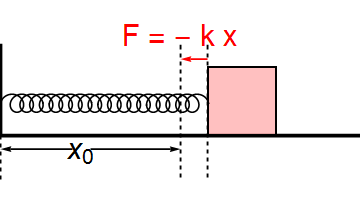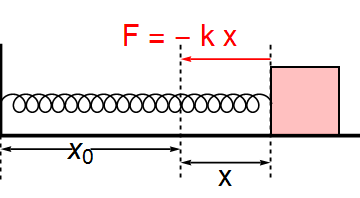
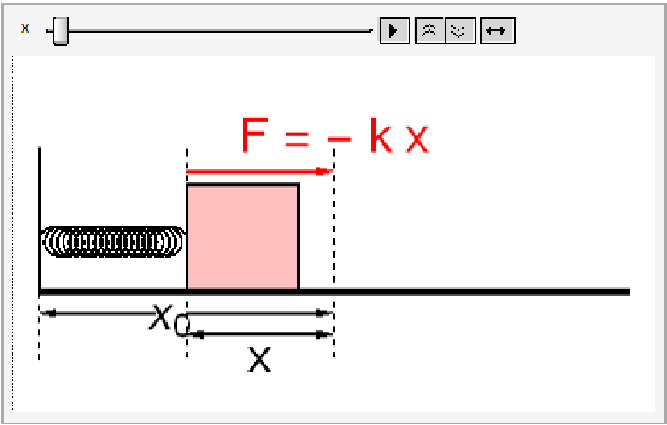
The result for this reasonably represents the motion of the block on the smooth floor (with scope of improvement :))