Imagine you have a set of geo positions that outline a path and you need to find all ZIP cods within 5 ml distance from this path. GeoNearest computation might time out due to complexity even for a single geo position, and even more so for, say, a few hundreds of them along a path. The computation is hard, because it involves lots of intersections with the ZIPCode polygons. But there is an easy work around via GeoEntities suggested here. I will show how to generalize it to a path. Import the data (attached) and extract positions:

data = Import["Line2.kml"];
pos = First[Cases[data, _GeoPosition, Infinity]]

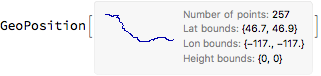
Sample 5 ml geo discs along the path in am optimal step: not to small to be redundantly overlapping and not too large to have gaps in coverage:

disks = GeoDisk[GeoPosition[#], Quantity[5, "Miles"]] & /@ pos[[1, 1 ;; -1 ;; 30]]

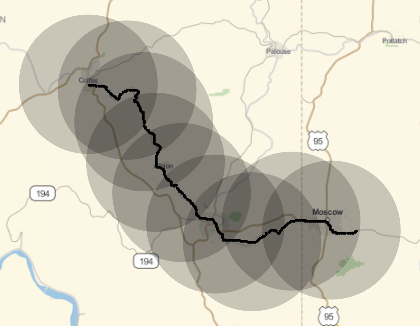
As we can see this is pretty good coverage:

GeoGraphics[{disks, Point[pos]}]

But why at step 30 ? Well first it could be trial and error. But simple calculations show the same. We need number of points long the path (for disk centers):

Length[First[pos]]
(* 257 *)

Length of path in miles:

UnitConvert[GeoLength[GeoPath[pos]], "Miles"]
(* Quantity[29.52736447128438`, "Miles"] *)

And now the upper bound for step which I then decreased a bit to 30 for better coverage:

Length[First[pos]] Quantity[5, "Miles"]/UnitConvert[GeoLength[GeoPath[pos]], "Miles"]
(*43.51895345247198`*)

Now easily get all ZIPs with GeoEntities:

zips = Flatten[GeoEntities[disks, "ZIPCode"]]

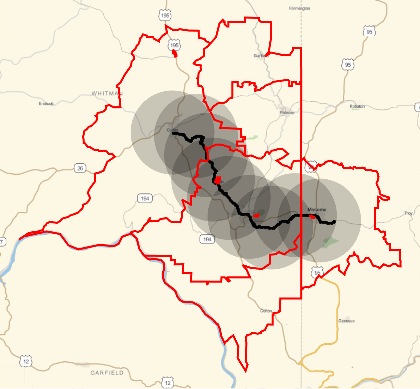
and visualize the result. We take Union below to remove duplicates. Note high diversity of ZIP regions sizes. ZIP regions obviously span beyond the disks, but all disks are contained within most outer border of ZIPs - so we did not miss anything.

GeoGraphics[{disks, Point[pos], {EdgeForm[{Red, Thick}], FaceForm[], Polygon[Union[zips]]}}]

Attachments: