It does not appear easy within the current Classify, Predict or NetTrain functions to accommodate weighted data. It I am wrong about this, can anyone tell me how to do so. If anyone has a work around, could you please make a suggestion.

Motivation: I have several projects that would benefit from weighted data, the latest being to explain this really interesting paper using Mathematica: https://arxiv.org/pdf/1602.04938.pdf . The idea would basically be to emulate one machine learning method -- the complex one such as a neural net -- with a less opaque one (such as a decision tree) but with the emulator only being responsible for producing similar answers within a neighborhood of certain points. This way one could use something close to human language to explain what a more complex and more opaque classifier was doing.

I'm attaching a draft notebook that shows some preliminary work in this field and indicates where having a weighted classifier would be an improvement.

SP - Lime: Emulating An Opaque Classifier With A Transparent One

Create a very complex function

Create a function that converts a vector into two numbers with a complex function.

nc = NetInitialize@NetChain[{50, ElementwiseLayer[Sin[Cos[#]] &], 2}, "Input" -> 20]

And convert two numbers into a Boolean classification likewise based on a complex function.

border[{x_, y_}] := Sin[3 (x + Cos[2 y - x])] > 0
RegionPlot[border[{x, y}], {x, -5, 5}, {y, -5, 5}]

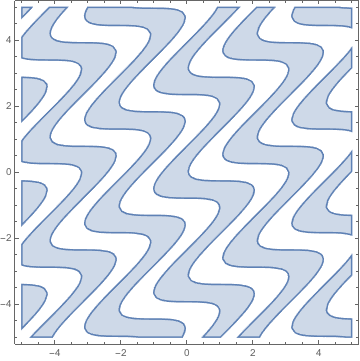
Compose the two functions

f[x_] := border[nc[x]]

Create some data

Create 10000 random instances

rv = RandomVariate[NormalDistribution[], {10000, 20}];

And now use the composite function to find out the truth.

data = rv -> Map[If[border[nc[#]], "evil", "good"] &, rv]

training = data[[1, 1 ;; 7500]] -> data[[2, 1 ;; 7500]]

test = data[[1, 7501 ;; 10000]] -> data[[2, 7501 ;; 10000]]

Learn the True Relationship from the Data

Try a simple classifier

simple = Classify[training, Method -> "DecisionTree", PerformanceGoal -> "Speed", ValidationSet -> test]

simplecmo = ClassifierMeasurements[simple, test]

simplecmo["Accuracy"]

0.7216

Create an Opaque But Better Classifier

Create a complicated neural network.

net = NetChain[{20, Ramp, 6, 2, SoftmaxLayer[]}, "Input" -> 20, "Output" -> NetDecoder[{"Class", {"evil", "good"}}]]

Train the network

netTrained = NetTrain[net, training, ValidationSet -> Scaled[0.25]]

See how well we did

clmo = ClassifierMeasurements[netTrained, test]

clmo["Accuracy"]

0.8312

clmo["CohenKappa"]

0.233322

Now create an emulator of the classifier

The idea of our emulator is not to predict reality but to explain what the complex classifier is doing!

Create new training data

training2 = First@training -> netTrained[First@training]

Create a nearest function so that we can only look at points in the neighborhood of a particular point. What I would prefer to do, but can not is to weight the data so that points closer to our particular point were weighted more heavily.

nf = Nearest[First@training -> Automatic]

Pick an arbitrary person (person 343) to whom we want to explain how our complex machine learning algorithm performed.

Short[neighborhoodData =  With[{nearest = nf[test[[1, 343]], 50]}, Part[training[[1]], nearest] -> Part[training[[2]], nearest]], 10]

Create a simple decision tree to emulate the complex classifier within the neighborhood of person 343.

clEmulator = Classify[neighborhoodData, Method -> "DecisionTree", PerformanceGoal -> "Speed"]

See how we did

clmo = ClassifierMeasurements[clEmulator, neighborhoodData]

clmo["ConfusionMatrixPlot"]

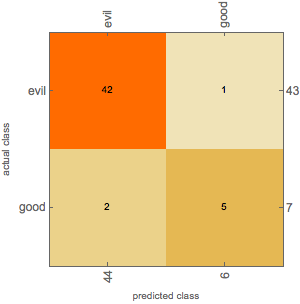
Our emulator explains 47 of the 50 decisions well.