A configuration is a set of points and lines such that $n$ points are on each line and $n$ lines go through each point. Here are a few 4-configurations: 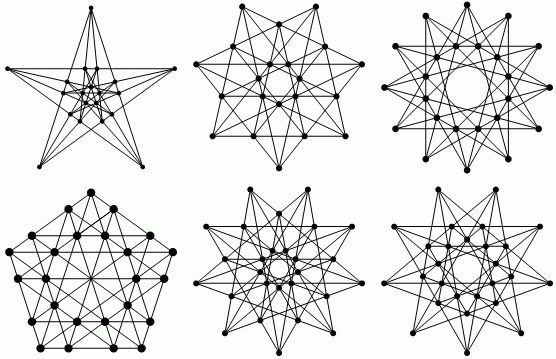
In barycentric coordinates, both lines and points can be represented as triples. If point $P$ is on line $L$, then the dot product $P.L=0$. For awhile now I've wondered if a self-dual barycentric configuration existed where the point set and line set used the same set of triples. The answer is YES, they exist. Here's a $24_3$ configuration. I've found about 120 of these.
set243 = {{-1, 1, 2}, {-1, 2, 1}, {-1, 2, 3}, {-1, 2, 4}, {-1, 3, 2}, {-1, 4, 2}, {0, 1, 2}, {0, 2, 1}, {1, 2, -1}, {2, 1, -1}, {2, 3, -1}, {2, 4, -1}, {3, 2, -1}, {4, 2, -1}, {1, 2, 0}, {2, 1, 0}, {2, -1, 1}, {1, -1, 2}, {3, -1, 2}, {4, -1, 2}, {2, -1, 3}, {2, -1, 4}, {2, 0, 1}, {1, 0, 2}};
tri=Reverse[{{Sqrt[3]/2,-(1/2)},{0,1},{-(Sqrt[3]/2),-(1/2)}}];
FromBarycentrics[{m_,n_,o_},{{x1_,y1_},{x2_,y2_},{x3_,y3_}}]:={m*x1+n*x2+(1-m-n)*x3,m*y1+n*y2+(1-m-n)*y3};With[{full=Union[Flatten[{#, RotateRight[#,1],RotateLeft[#,1]}&/@{{-1,1,2},{-1,2,1},{-1,2,3},{-1,2,4},{-1,3,2},{-1,4,2},{0,1,2},{0,2,1}},1]]},
Graphics[{EdgeForm[Black],Tooltip[Line[#[[2]]],Style[Row[Switch[Sign[#],-1,Style[ToString[Abs[#]],Red],0,Style[ToString[Abs[#]],Darker[Green]],1,Style[ToString[Abs[#]],Blue]]&/@#[[1]]],16,Bold]]&/@Table[{full[[k]],Sort[FromBarycentrics[#/Total[#],tri]&/@Select[full,full[[k]].#==0&]]},{k,1,Length[full]}],White,{Disk[FromBarycentrics[#/Total[#],tri],.075],Black, Style[Text[Row[Switch[Sign[#],-1,Style[ToString[Abs[#]],Red],0,Style[ToString[Abs[#]],Darker[Green]],1,Style[ToString[Abs[#]],Blue]]&/@#],FromBarycentrics[#/Total[#],tri]],16,Bold]}&/@full}]]
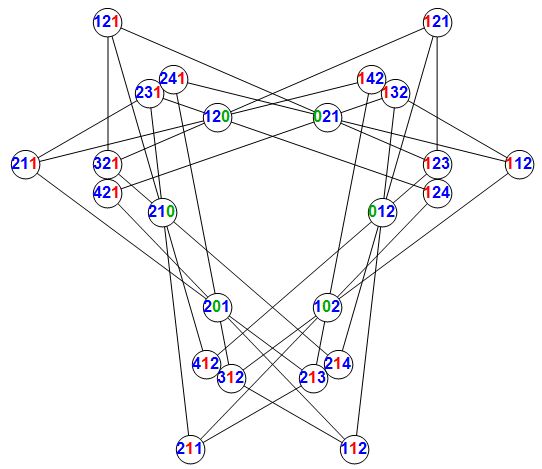
I also found a single $27_4$ configuration.
config274={
{-2,-1,4},{-2,1,3},{-1,1,1},{-1,2,0},{-1,2,1},{-1,3,2},{-1,4,2},{0,1,2},{1,1,2},
{-1,4,-2},{1,3,-2},{1,1,-1},{2,0,-1},{2,1,-1},{3,2,-1},{4,2,-1},{1,2,0},{1,2,1},
{4,-2,-1},{3,-2,1},{1,-1,1},{0,-1,2},{1,-1,2},{2,-1,3},{2,-1,4},{2,0,1},{2,1,1}}
With[{full=Union[Flatten[{#, RotateRight[#,1],RotateLeft[#,1]}&/@{{-2,-1,4},{-2,1,3},{-1,1,1},{-1,2,0},{-1,2,1},{-1,3,2},{-1,4,2},{0,1,2},{1,1,2}},1]]},
Graphics[{EdgeForm[Black],Tooltip[Line[#[[2]]],Style[Row[Switch[Sign[#],-1,Style[ToString[Abs[#]],Red],0,Style[ToString[Abs[#]],Darker[Green]],1,Style[ToString[Abs[#]],Blue]]&/@#[[1]]],16,Bold]]&/@Table[{full[[k]],Sort[FromBarycentrics[#/Total[#],tri]&/@Select[full,full[[k]].#==0&]]},{k,1,Length[full]}],White,{Disk[FromBarycentrics[#/Total[#],tri],.07],Black, Style[Text[Row[Switch[Sign[#],-1,Style[ToString[Abs[#]],Red],0,Style[ToString[Abs[#]],Darker[Green]],1,Style[ToString[Abs[#]],Blue]]&/@#],FromBarycentrics[#/Total[#],tri]],7]}&/@full}]]
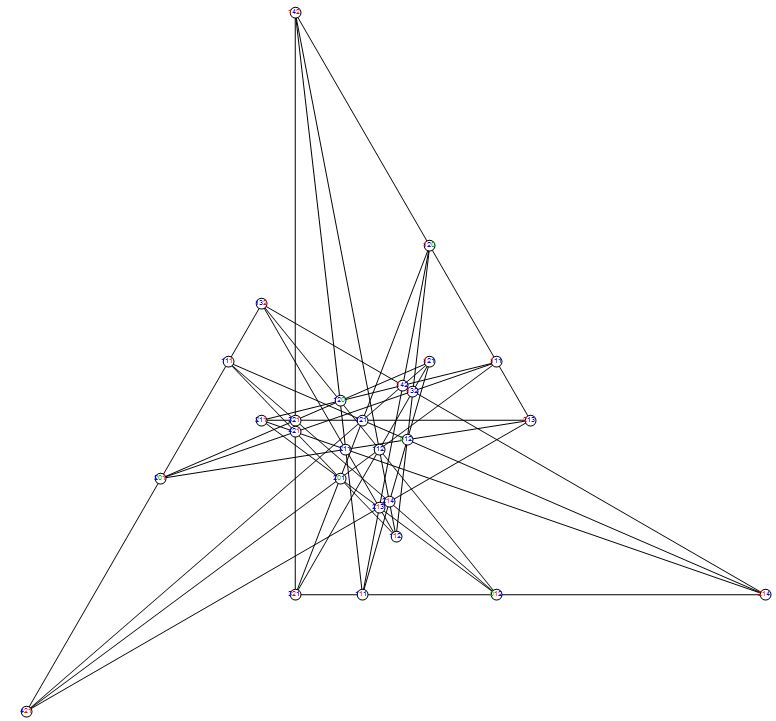
It's easy to check. The following code gives a list of 27 4's.
Length /@ Table[Select[config274, config274[[n]].# == 0 &], {n, 1, 27}]
We can make a graph of these triples.
Graph[#[[1]] <-> #[[2]] & /@ Select[Subsets[Sort[config274], {2}], #[[1]].#[[2]] == 0 &], VertexLabels -> "Name"]
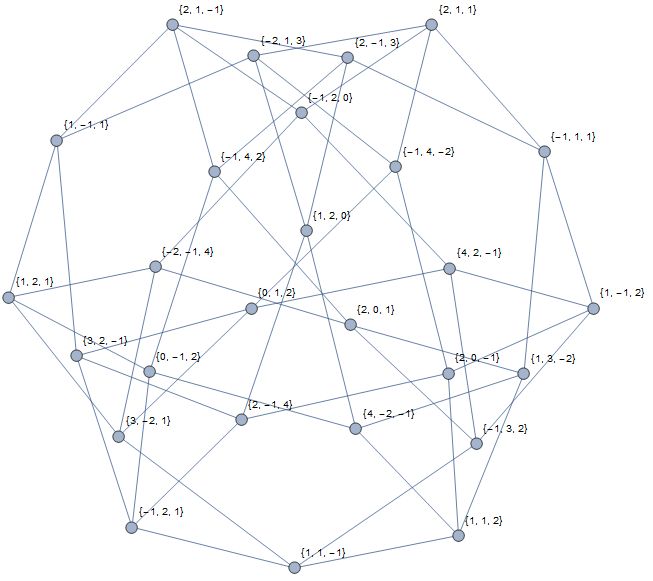
Whether there is a 5-configuration with this method is something I'm still running.
 Attachments:
Attachments: