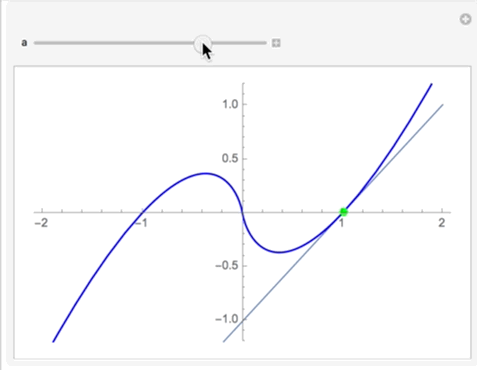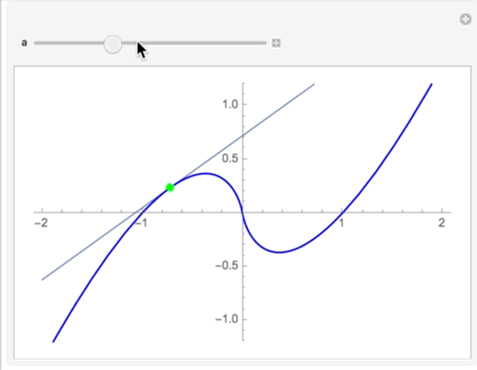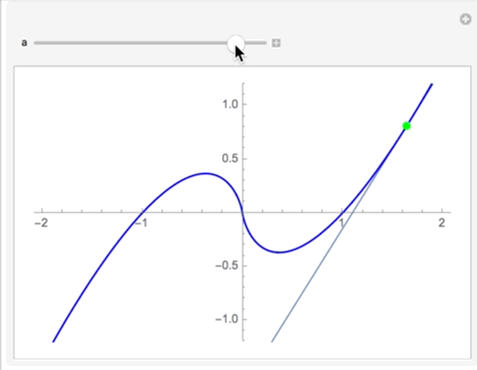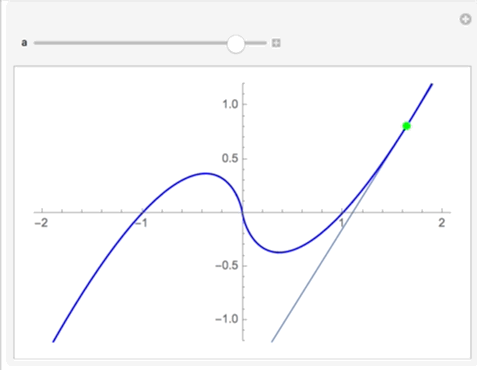
Clement, you should post code using the code formatting box (upper left icon) so it is more useful and readable when you post. Your function is indeterminate at x=0, however if you take the Limit[ ] as x->0 it goes to 0 as x->0. Using this fact you can construct a peicewise function and manipulate it:
g[x_] := Piecewise[{{x*Log[x], x > 0}, {x*Log[-x], x < 0}, {0,
x == 0}}]; Manipulate[
With[{tl = Normal@Series[g[x], {x, a, 1}]},
Show[Plot[{tl, g[x]}, {x, -2, 2},
PlotStyle -> {Thickness[0.003], Blue}, PlotRange -> {-1.2, 1.2}],
Graphics[{Green, PointSize[0.02], Point[{a, g[a]}]}]]], {{a,
1}, -2, 2}]
This gives you the plot of the function and its tangent. The trick with the Normal@Series[g[x],{x,a,1}]... generates the Taylor series out to the first derivative and chops it at the first derivative. (I saw this on a post here once but I do not remember who posted it -- apologies to the clever author!). This is a cool way to get the tangent because you always get a function for a line -- its independent of the function whereas derivative will be a general function and you then must construct a line.
