I love how Mathematica lets you create endless animations with just a tiny bit of code. Here is a short hypnocode with iterative image processing:
a = RandomReal[1, 200 {1, 1}]; Dynamic[Image[a = Rescale[a - GradientFilter[a, 2, Method -> "Sobel"]]]]
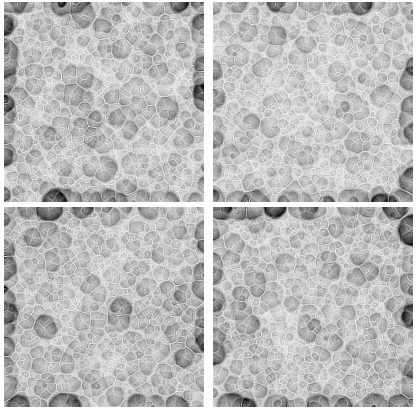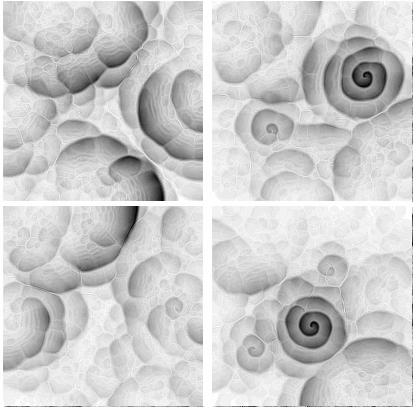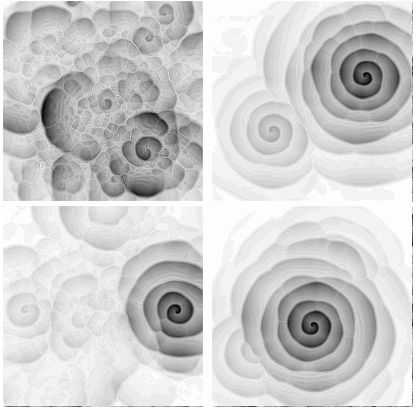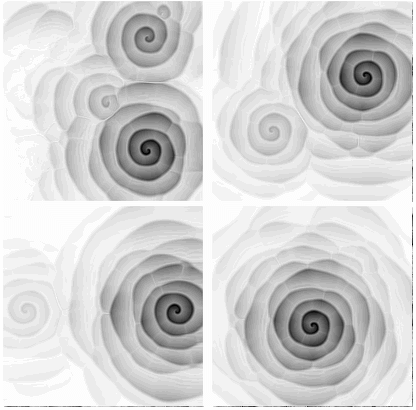
For symmetric initial conditions such as DiskMatrix[10, 200] the asymmetry appears after just one iteration of the filter. I guess the swirling rose is stable with respect to small numerical errors. I was unable to find any initial condition which didn't eventually lead to it, but there may well be other stable states that we haven't seen yet. Not exact arithmetic, but a bit of rounding makes it interesting...
a = DiskMatrix[10, 200];
Dynamic[Image[a = Rescale[Round[a - GradientFilter[a, 2, Method -> "Sobel"], 0.09]]]]
For no particularly good reason, I made a version of my iterative gradient filter on a 3D image. It doesn't run very fast, as you might imagine, so I
uploaded also a movie here.
i = RandomReal[{0, 1}, {100, 100, 100}];
Do[i = Rescale[i - GradientFilter[i, 2]]; t = 2 Pi j/300.;
Export["image_" <> ToString[j] <> ".bmp",
Rasterize[Image3D[i^10, ViewPoint -> {3 Cos[t], 3 Sin[t], 2},
SphericalRegion -> True], ImageSize -> {300, 300}]], {j, 800}]
