It does not work because

In[2]:= RecurrenceTable[{a[n + 1] == 1/2 (-(1/a[n]) + a[n]), a[1] == 42}, a, {n, 1, Infinity}]
During evaluation of In[2]:= RecurrenceTable::eternal: -- Message text not found -- >>

Out[2]= RecurrenceTable[{a[1 + n] == 1/2 (-(1/a[n]) + a[n]),  a[1] == 42}, a, {n, 1, \[Infinity]}]

RecurrenceTable does not return a list of numerical values, because one cannot have an infinite list as output. It is

In[1]:= RecurrenceTable[{a[n + 1] == 1/2 (-(1/a[n]) + a[n]),  a[1] == 42}, a, {n, 1, 19}] // N
Out[1]= {42., 20.9881, 10.4702, 5.18736, 2.49729, 1.04843, 0.0473099, \
-10.545, -5.22506, -2.51684, -1.05976, -0.0580726, 8.58087, 4.23217, \
1.99794, 0.748712, -0.293457, 1.5571, 0.457438}

RecurrenceTable[] as such isn't necessary, one might use

In[52]:= Remove[f]
f[1] = 42.;
f[n_Integer /; n > 1] := f[n] = (f[n - 1] - 1/f[n - 1])/2

In[56]:= Union[Chop[Table[f[o], {o, 1, 19}] - %1]]
Out[56]= {0}

In[55]:= f[1000]
Out[55]= -3.13826

If one defines

f[1]=42

then also this function remembering its values will not return in useful time because the integers involved become too big for big arguments. One might want to read Limits without Limits in Version 11.2 to find out something about f. If you look at the values that way, forming 2-tuples

In[69]:= ListPlot[Table[{f[o], f[o + 1]}, {o, 2, 2000, 2}]]

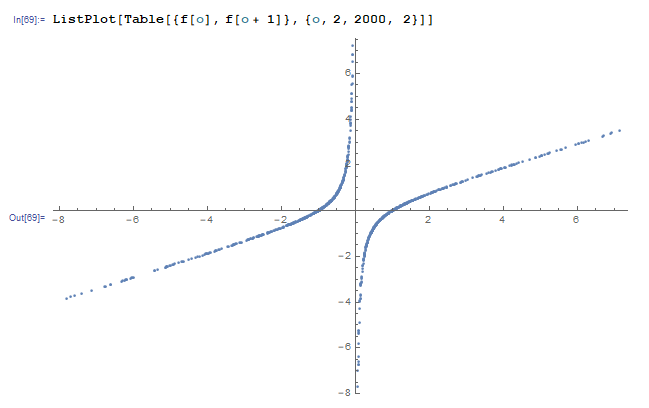
you are possibly able to find and enter a correct analytic approximation into this famous Zeta to step forward with your problem.

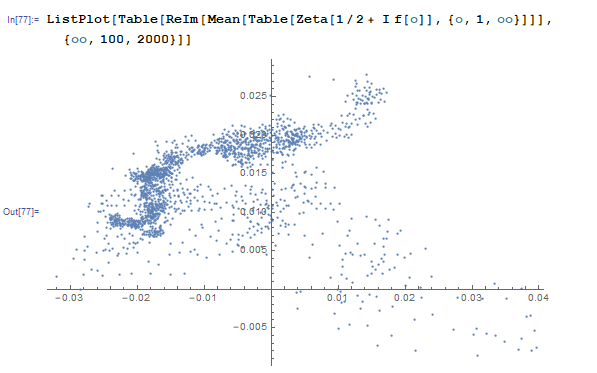
Without it you can generate data like this

In[77]:= ListPlot[Table[ReIm[Mean[Table[Zeta[1/2 + I f[o]], {o, 1, oo}]]], {oo, 100, 2000}]]

but I'm affraid it might mean just nothing: