Message Boards Message Boards

0
|
11684 Views
|
6 Replies
|
4 Total Likes
View groups...
Share
Share this post:

Correct format for NetChain?

Lenny Johnson
Posted 7 years ago

I am trying to create a simple neural network with one hidden layer to recognise hand written characters from the MNIST training set. I would like my hidden layer to be an ElementwiseLayer[LogisticSigmoid] with 30 neurons. I would have expected the syntax for a linear layer to be

NetChain[{LinearLayer[30]}, 
 "Input" -> NetEncoder[{"Image", {28, 28}, "Grayscale"}], 
 "Output" -> NetDecoder[{"Class", Range[0, 9]}]]

But this generates the error

"Specification NetDecoder[Class, ...]) is not compatible with port "Output", which must be a length-30 vector"

Does anyone have an idea what the correct syntax is to achieve what I want?

Thanks
POSTED BY: Lenny Johnson
6 Replies
Sort By:

Your NetChain outputs a vector of length 30, and you are trying to feed this into a NetDecoder that expecting only 10 inputs. Hence the error. So something like this will work:

NetChain[{LinearLayer[10]}, 
 "Input" -> NetEncoder[{"Image", {28, 28}, "Grayscale"}], 
 "Output" -> NetDecoder[{"Class", Range[0, 9]}]]
POSTED BY: Sebastian Bodenstein

Lenny, you may need to add SoftmaxLayer. So something like this will work:

testNet = 
 NetChain[{LinearLayer[10], SoftmaxLayer[]}, 
  "Input" -> NetEncoder[{"Image", {28, 28}, "Grayscale"}], 
  "Output" -> NetDecoder[{"Class", Range[0, 9]}]]

I've tried this. The accuracy was 0.7621 because of a simple neural network.

trainedNet = 
  NetTrain[testNet, trainingData, BatchSize -> 1000, 
   MaxTrainingRounds -> 1];
cm = ClassifierMeasurements[trainedNet, testData];
cm["Accuracy"]
POSTED BY: Kotaro Okazaki

This net does not have an explicit loss function, so a loss function will be chosen automatically based on the final layer or layers in the net.

The Details and Options of CrossEntropyLossLayer Help say,

When appropriate, CrossEntropyLossLayer is automatically used by NetTrain if an explicit loss specification is not provided. One of "Binary", "Probabilities", or "Index" will be chosen based on the final activation used for the output port and the form of any attached NetDecoder.

and

For CrossEntropyLossLayer["Index"], the input should be a vector of probabilities {p1,...,pc} that sums to 1, or a tensor of such vectors. The target should be an integer between 1 and c, or a tensor of such integers."

So, I think this net needs SoftmaxLayer for NetTrain.
POSTED BY: Kotaro Okazaki
Lenny Johnson
Lenny Johnson
Posted 7 years ago

Thanks. I had misinterpreted the Output decoder as actually creating an output layer. Using the above network seems to generating an error when attempting to train the network. 

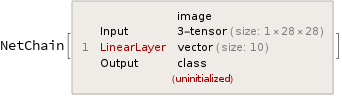
testNet =NetChain[{LinearLayer[10]}, 
 "Input" -> NetEncoder[{"Image", {28, 28}, "Grayscale"}], 
 "Output" -> NetDecoder[{"Class", Range[0, 9]}]]

enter image description here

myResource = ResourceObject["MNIST"];
trainingData = ResourceData[myResource, "TrainingData"];
testData = ResourceData[myResource."TestData"];
testNet = NetInitialize[testNet]

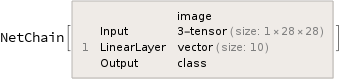
enter image description here

trainedNet = 
 NetTrain[testNet, trainingData, BatchSize -> 1000, 
  MaxTrainingRounds -> 1]

This generates the error...

NetTrain::invindim: Data provided to port "Output" should be a list of length-10 vectors.

A simple validation to check if the net is receiving data and output an expected type appears correct.

testNet[Keys[trainingData[[1]]]]
1

Obviously the network is not trained so the output digit may be incorrect but it is a scalar in our range 0-9.

Do you have any ideas why the it believes the output data is not of the correct length?
POSTED BY: Lenny Johnson
Lenny Johnson
Lenny Johnson
Posted 7 years ago

Thank you for the information. Indeed it does seem to allow the network to train. Do you know why the addition of the SoftMaxLayer was required? I have checked the documentation for NetDecoder and it does not seem to indicate it as a requirement. The output of the final layer has to be a vector ( or more generally a tensor) that matches the number of class types. I can appreciate how the SoftMaxLayer would make deciding which class element to choose but it is not specified as being required.

POSTED BY: Lenny Johnson
Lenny Johnson
Lenny Johnson
Posted 7 years ago

That seems like a plausible explanation. The answer is in the details.

Thank you.
POSTED BY: Lenny Johnson
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract