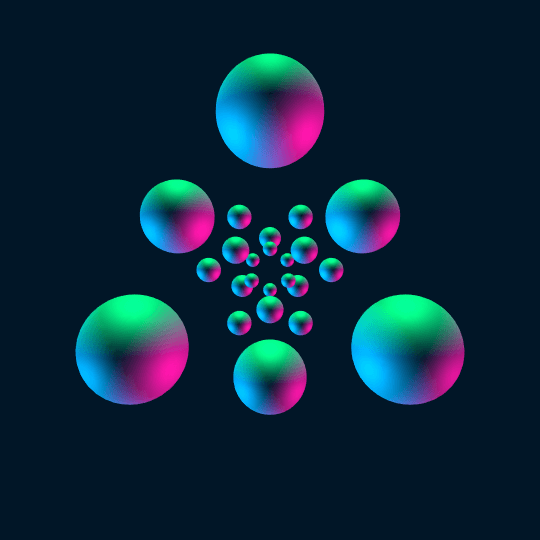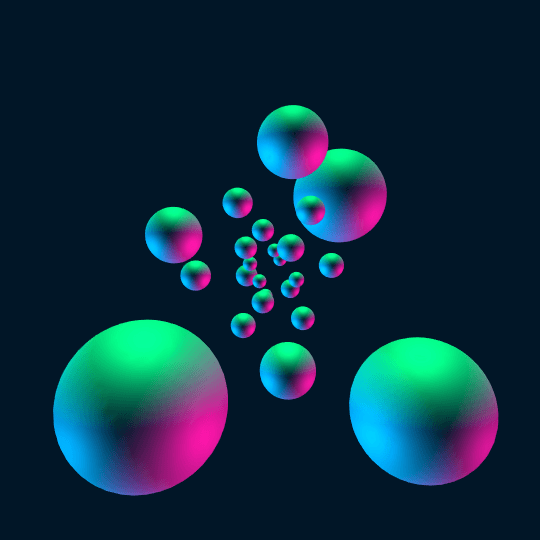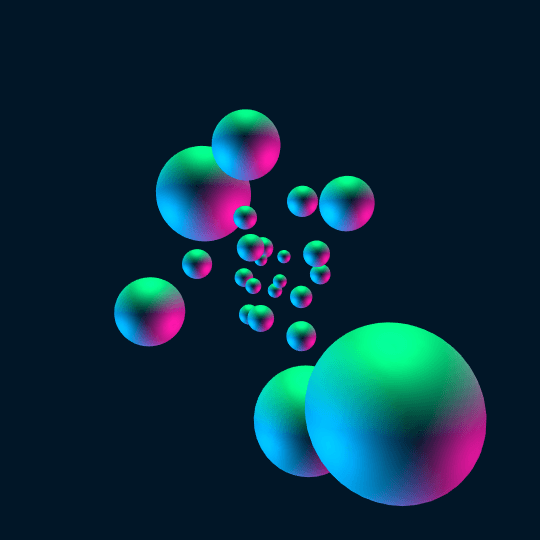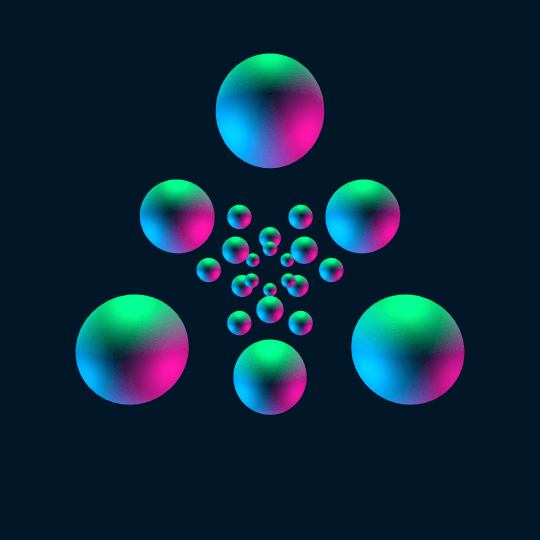
All Day

Same idea as Touch ’Em All: this is the stereographic image of a Hamiltonian cycle on the 24-cell. The idea behind the code is the same, so look back at that post for an explanation (as before, the definition of ProjectedSphere[] is not reproduced here; see Inside).

Stereo[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)}

smootherstep[t_] := 6 t^5 - 15 t^4 + 10 t^3;

twenty4cellvertices = Normalize /@
   DeleteDuplicates[
    Flatten[
     Permutations /@ ({-1, -1, 0, 0}^Join[#, {1, 1}] & /@ Tuples[{0, 1}, 2]), 1]
    ];

sorted24CellVertices = 
  Module[{v = twenty4cellvertices, M, ?, cycle},
   M = Table[
     If[v[[i]] != -v[[j]] && HammingDistance[v[[i]], v[[j]]] == 2, 1, 
      0], {i, 1, Length[v]}, {j, 1, Length[v]}];
   ? = AdjacencyGraph[M];
   cycle = FindHamiltonianCycle[?];
   v[[#[[1]] & /@ (cycle[[1]] /. UndirectedEdge -> List)]]
   ];

DynamicModule[{?, viewpoint = 1/2 {-1, 1, 1}, 
  pts = N[sorted24CellVertices], 
  cols = RGBColor /@ {"#04E762", "#00A1E4", "#DC0073", "#011627"}},
 Manipulate[
  ? = ?/3 smootherstep[t];
  Graphics3D[{Specularity[.4, 10],
    Table[
     ProjectedSphere[RotationMatrix[?, {pts[[i]], pts[[Mod[i + 1, Length[pts], 1]]]}].pts[[i]], .2],
     {i, 1, Length[pts]}]},
   PlotRange -> 4.5, ViewAngle -> ?/3, ViewPoint -> viewpoint, 
   Boxed -> False, Background -> cols[[-1]], ImageSize -> 540,
   Lighting -> {{"Directional", cols[[1]], 
      50 {1, -1, 2}}, {"Directional", cols[[2]], 
      50 {1, 2, -1}}, {"Directional", cols[[3]], 
      50 {-2, -1, -1}}, {"Ambient", cols[[-1]]}}],
  {t, 0, 1}]
 ]