It seems to me that your principal objective here is to write tutorials by presenting derivations and proofs in a clear manner but have somehow gotten a little bit on a false path. But your examples are too simple to make clear how you want to present them by "searching for patterns". Let's take the Pauli matrix example. We could define numeric and symbolic variables.

PMat1 = {{0, 1}, {1, 0}};
PMat2 = {{0, -I}, {I, 0}};
PMat3 = {{1, 0}, {0, -1}};
symbolicRules = 
 Thread[{\[Sigma]1, \[Sigma]2, \[Sigma]3} -> 
   MatrixForm /@ {PMat1, PMat2, PMat3}] 

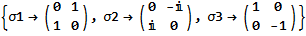
Then we can do a simple validation of the identity. We can add annotation for the steps. The Mathematica Inactive and Activate commands are very useful for step by step derivations. (But I don't like the light red font for the Inactive command and changed my style sheet to regular black. WRI used to have a Tooltip to identify Inactive commands but seem to have taken that away.)

simpleDerivation =
 pagelet[
  phrase2["Pauli matrix identity:"],
  step1 = Inactive[Equal][\[Sigma]1.\[Sigma]2, I \[Sigma]3],
  phrase2["Substitute the numeric Pauli matrices."],
  step2 = step1 /. symbolicRules,
  phrase2["Evaluate"],
  step3 = Activate[step2] /. MatrixForm -> Identity,
  Spacings -> 1.25
  ]

So, is that good enough for your readers? Here is a second derivation.

secondDerivation =
 pagelet[
  phrase2["Pauli matrix identity:"],
  step1 = Inactive[Equal][\[Sigma]1.\[Sigma]2, I \[Sigma]3],
  phrase2["Substitute the numeric Pauli matrices."],
  step2 = step1 /. symbolicRules,
  phrase2["Factor \[ImaginaryI] from \[Sigma]2 and the product."],
  step3 = 
   step2 /. \[Sigma]2 : MatrixForm[PMat2] -> 
     FactorOut[I, MatrixForm][PMat2],
  step4 = MapAt[LinearBreakout[Dot][_], step3, 1],
  phrase2["Evaluate the left hand side and then the equality."],
  step5 = 
   step4 // EvaluateAt[1, (MatrixForm[# /. MatrixForm -> Identity] &)],
  step6 = Activate[step5] /. MatrixForm -> Identity,
  Spacings -> 1.25
  ]

I've used a number of constructs from a Presentations application that I've developed over the years. The phrase and pagelet routines are just Row and Column constructs without the extra brackets. FactorOut will remove a factor from a larger expression. LinearBreakout is useful in expanding and factoring out constants from "linear" expressions.

There are also routines for defining subexpressions and holding them unevaluated in Mathematica simplifications. Also a set of routines for primitive operations on annotated matrix structures, mostly for didactic purposes. If you contact me, and tell me something about yourself, I can send a download link.

You should understand that evaluation in the Wolfram Language means something like I PauliMatrix[3] will automatically become an explicit matrix {I, 0}, {0, -I}}. There are ways to preclude this using Hold but they are more trouble than they are worth. An alternative route might be to work with your own purely symbolic pauliMatrix (note lower casing of first word, to distinguish from the built-in function). When you want to do symbolic manipulations you might use NonCommutativeMultiply as operator, and only when you want to convert to explicit matrices do you use substitutions such as {NonCommutativeMultiply->Dot,pauliMatrix->PauliMatrix}.

Also for the purpose at hand you might want to consider introducing a commutator, so that the comcommutative products can be "canonicalized" prior to using a substitution such as this: pauliMatrix[1] ** pauliMatrix[2] -> I*pauliMatrix[3]. One way to go about this is shown here.

https://www.researchgate.net/publication/262223580_Symbolic_FAQ

See the section "Some noncommutative algebraic manipulation", in particular the example that defines and uses a function called ncTimes.

Thanks Daniel,

What I meant was, can I make Mathematica recognise PauliMatrix[1].PauliMarix[2] as I PauliMatrix[3]? So rather than answer {{I, 0}, {0, -I}} it would say I PauliMatrix[3] (and ultimately use the sigma symbols I have defined)?

I guess it would be similar in simpler expressions. Suppose I defined

a = x+3

how would I make Mathematica reduce

x^2 + 9 + 6x

to

a^2

?