Eric,

I hadn't seen your other thread. I just glanced at it. I can give a few comments on Mathematica's notation vs engineering notation. I think it is fine that you are creating a way to convert between the two. However, I don't have a problem with using or interpreting Mathematica's notation. It is standard, accepted math notation, after all. I say that as a former EE who was taught engineering notation. The downside of the conversion is that it adds another layer of notation. It may also lead to undesirable side effects. For those reasons, I doubt that I would find it useful.

I wasn't currently working on any Boolean related functionality. I happened to see this thread about function names and thought it might be interesting to see the reason for the question and the replies. After understanding what you were actually trying to implement, I thought it would be useful to see if I could implement a JK FF in MMA. I read Neil's suggestion to use SystemModeler, but a full license for that is unreasonably expensive for an individual (my opinion). I have the Home licensed version of SystemModeler, but it is not being kept updated as far as I know. You also mentioned that you would like to implement the MMA version as a learning experience. So, I came up with something very rudimentary in MMA. I used very limited error checking. I haven't thought much about how I would model connecting these FF's in a circuit and sequence them with a clock. Obviously, it would be a significant abstraction from real world hardware. I'm sure what I implemented could be improved, but I'm happy with my first attempt. Good luck with you investigations.

Eric,

You can take a look at the following. I think it gives a start on implementing the functionality that you desire. MMA has some nice Boolean logic functionality built in to make this easier.

First, I create a characteristic equation for the JK FF. Then, create a BooleanFunction to implement the corresponding truth table:

jkFFEqn = (j \[And] \[Not] q) || (\[Not] k \[And] q)
jkFlipFlop = BooleanFunction[BooleanTable[jkFFEqn, {j, k, q}]]

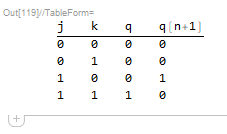
Confirm that the correct truth table is generated:

TableForm[
 Boole@BooleanTable[{j, k, q, jkFlipFlop[j, k, q]}, {j, k, q}], 
 TableHeadings -> {None, {j, k, q, "q[n+1]"}}]

This function will generate the transition to the next state. It requires that the flip flop to be transitioned be initialized to a known state. Note: I made some changes force the flip flop object state to be a Boolean value (True, False). This will make it unnecessary to convert (0, 1) values to (False, True) when chaining negated outputs to inputs.

Clear[jkFlipFlopNextState]

jkFlipFlopNextState[j_?(# == 0 || # == 1 &), k_?(# == 0 || # == 1 &), 
  flipflopObj_Symbol, id_Integer] := 
 jkFlipFlopNextState[j != 0, k != 0, flipflopObj, id] /; 
  ValueQ[flipflopObj[id]]

jkFlipFlopNextState[j_?(# == 0 || # == 1 &), 
  k_?(# == False || # == True &), flipflopObj_Symbol, id_Integer] := 
 jkFlipFlopNextState[j != 0, k, flipflopObj, id] /; 
  ValueQ[flipflopObj[id]]

jkFlipFlopNextState[j_?(# == False || # == True &), 
  k_?(# == 0 || # == 1 &), flipflopObj_Symbol, id_Integer] := 
 jkFlipFlopNextState[j, k != 0, flipflopObj, id] /; 
  ValueQ[flipflopObj[id]]

jkFlipFlopNextState[j_?(# == False || # == True &), 
  k_?(# == False || # == True &), flipflopObj_Symbol, 
  id_Integer] := (flipflopObj[id] = 
    jkFlipFlop[j, k, flipflopObj[id]]) /; (flipflopObj[id] == False ||
     flipflopObj[id] == True)

To test, pick a name for your JK FF and a unique integer ID and an initial output (Q) state. I choose False as the initial state:

jkFF[1] = False

Then, run the state transition function. I generated some test input pairs (J, K) and mapped the transition function onto that list:

TableForm[{#[[1]], #[[2]], Boole@jkFF[1], 
    Boole@jkFlipFlopNextState[#[[1]], #[[2]],jkFF, 1]} & /@ Tuples[{0, 1}, 2], 
 TableHeadings -> {None, {j, k, q, "q[n+1]"}}]

You can add more JK's simply by initializing them like I did for jkFF[1], Like this,

jkFF[2] = False (* This could be False or True *)
jkFF[3] = True (* etc, etc *)

Here's a JK FF configured as a toggler.

jkFF[1] = False;
Table[Boole@jkFlipFlopNextState[1,1, jkFF, 1], 10]
Out[125]:= {1, 0, 1, 0, 1, 0, 1, 0, 1, 0}

I didn't implement the clock since that seems to be a relatively simple extension to what I've done. If you desire, you can put all of this in a context (package) for localization. Hope this helps.

But the big problem is: Why doesn't Mathematica support static variables?

Just a minor remark: On can easily mimic static variables like so:

Module[{static = 1},
 f[x_] := (static++) Sin[x]
 ]

This way static is global for the function f[], but only for f[], and so it appears to be static. From outside the respective Module it cannot be seen. If I remember correctly I have this idea from @Leonid Shifrin.

Best regards -- Henrik

The "Updating Name" is me. I get this every now and then. Does it happen to others?

One way to have a static variable is to use "subvalues" (definitions/calls of the form h[v1, v2,...][x]) to define methods on a data structure h[v1, v2,...]. Here's a simplified toggler. I use an Association for the data structure, but it could be any sort of variable. It's important to store the symbol and not its value in jk[s].

ClearAll[jk];
SetAttributes[jk, HoldAll];        (* must hold its arguments because s must be a Symbol in jk[s] *)
jk[] := With[{s = Unique["s"]}, s = <|"state" -> 0|>; jk[s]];   (* creates new toggler *)
jk[s_]["toggle"] := s["state"] = 1 - s["state"];                (* method to toggle state *)
jk[s_]["state"] := s["state"];                                  (* method to return state *)

jk1 = jk[]
jk1["state"]
(*  jk[s260]   the symbol s260 will be different each time *)
(*  0  *)

jk1["toggle"];
jk1["state"]
(*  1  *)

jk1["toggle"];
jk1["state"]
(*  0  *)

Since Mathematica does not have true local variables, the "static variable" is actually in the "Global`" context:

s260
(*  <|"state" -> 0|>  *)

To further protect the "localization," it is common to put these such variables in a special context. One could, say, have a "jkdump"`` context:

jk[] := With[{s = Unique["jkdump`s"]}, s = <|"state" -> 0|>; jk[s]];   (* creates new toggler *)

jk2 = jk[]
(*  jk[jkdump`s13]  *)

jk2["toggle"]
(*  1  *)

s13 
jkdump`s13
(*  s13  *)
(*  <|"state" -> 1|>  *)

When I tried your original code, nothing happened. Just tried it again, still nothing. But it obviously works.

When I run the code (from either my first or second post) on a fresh kernel, something happens, namely just what I showed. We must be running different things. Maybe you have a definition for test already in your kernel session or something like that. But I can't quite reconcile "nothing happened" with "it obviously works," so maybe you mean something else.

Eric,

Another all WMA way to do the FlipFlops is to avoid JK1=JKFlipFlop and do something like:

JKFlipFlop[name_, otherArgs]:=...

and use it

JKFlipFlop["JK1", otherArgs]

inside the definition you can do

Set[Evaluate[Symbol[name <> "State"]], whateverYouWant]

You can also use Unique[] to generate a new, unique symbol name.

Eric,

First of all. Just to explain Michael's code, there is nothing special about "call". He is using the pattern naming feature of the : symbol. Just as you can define

Test[x_]

is equivalent to

Test[x:_]

where the x:_ means "match anything and call it x". x_ is a shortcut for x : _

fun : Test[x_]

means Match Test[_] and put the held value of the entire expression in fun and put the stuff inside the Test into x.

The documentation on ":" can be found here and more info is in the docs about pattern matching which are referenced in that link.

Secondly, I think you should consider Wolfram's SystemModeler (WSM) for your application. It will out of the box model JKFlipFlops and you can interact with it from Mathematica (WMA). In fact you can programmatically create models with flipflops and run the simulations from WMA and get the results back in WMA. Here is an example from WSM where they have a JKFlipFlop (which was modeled with two RS FlipFlops and some logic):

Regards,

Neil

Can you elaborate on what is the final goal, desired usage and output for provided input?

E.g. I don't know why

test[x_] := Module[{testState}, whatever; testState = 67] 

does not fit your needs.

Not sure exactly what you're after, but this sets name to the held head of the function call:

call : test[x_] := Block[{x},
  Print[name = Hold@call /. Hold[f_[___]] :> Hold[f]];
  ToExpression["test" <> "State"];
  testState = 67]

test[a]
(*
  Hold[test]
  67
*)

name
(*  Hold[test]  *)

Not sure what the Block[{x}..] is for nor the ToExpression. They seem extraneous or confusing.