At Wheels of Powered Triangles I have various solutions to making a wheel out of similar triangles. Every edge is the power of a particular root. I recently decided to see if the polynomial discriminants would be interesting.

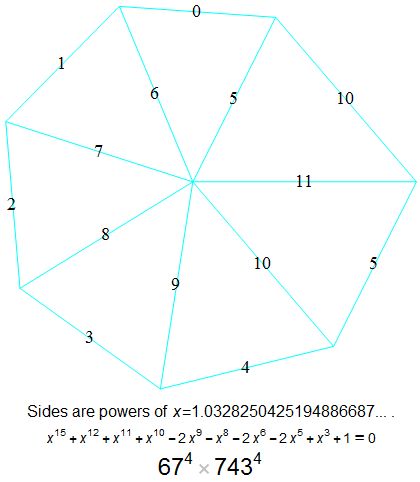
Here's a case that has all powers 0 to 11 in a regular pattern, with some repetition. We get two fourth powers.

$x^{15}+x^{12}+x^{11}+x^{10}-2 x^9-x^8-2 x^6-2 x^5+x^3+1==0$
Discriminant $67^4 \times 743^4$

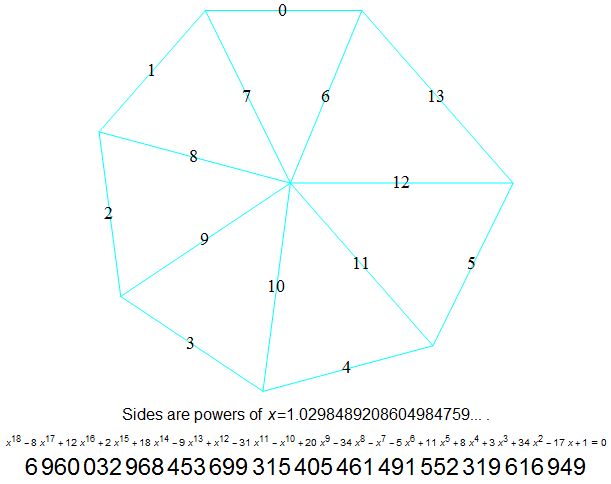
When the repetition is removed to give all powers 0 to 13 in the same pattern, we get a giant prime.

$x^{18}-8 x^{17}+12 x^{16}+2 x^{15}+18 x^{14}-9 x^{13}+x^{12}-31 x^{11}-x^{10}+20 x^9-34 x^8-x^7-5 x^6+11 x^5+8 x^4+3 x^3+34 x^2-17 x+1==0$
Discriminant is the prime $6960032968453699315405461491552319616949$